Introduction
Sequences and Summations না বলে যদি আমরা বলি ধারা এবং ধারার সমষ্টি তাহলে বোধহয় আমাদের কাছে অতি পরিচিত লাগে। হ্যাঁ আজ আমরা আমাদের সেই ছোটবেলার ধারা এবং সমষ্টি নিয়ে আলোচনা করবো। সিকোয়েন্স এবং সামেশন অনেক গুরুত্বপূর্ন ডাটা স্ট্রাকচার। আমরা বিভিন্ন কাউন্টিং প্রব্লেম সলভ করার জন্য এই মেথডগুলো ব্যবহার করি। এছাড়াও আমরা যারা প্রোগ্রামিং এর সাথে যুক্ত তাদের কাছে fibonacci numbers অনেক পরিচিত একটা টার্ম। সেই জিনিসটা সলভ করার জন্য আমরা এই সিকোয়েন্স এবং সামেশন ব্যবহার করি। এছাড়াও আরো অনেক ব্যবহার রয়েছে এর তা আমরা আস্তে আস্তে দেখতে পাবো। চলুন শুরু করা যাক।
Sequences
সিকোয়েন্স বা ধারা হলো একটা ডিসক্রিট স্ট্রাকচার যা একটা বিন্যস্ত লিস্ট বা তালিকা রিপ্রেজেন্ট করে। যেমন ১, ২, ৩, ৫, ৮ হলো ৫টা টার্মের একটা সিকোয়েন্স এবং ১, ৩, ৯, ৮১, ..., ৩^n, ... হলো একটা infinite sequence বা যাকে আমরা অনন্ত ধারা বলে চিনি। এর অফিসিয়াল সংজ্ঞাটা আমরা একটু নিচে দেখি।
A sequence is a function from a subset of the set of integers (usually either the set {0, 1, 2, …} or the set {1, 2, 3, …}) to a set S. We use the notation
anto denote the image of the integer n. We callana term of the sequence.
অর্থাৎ সিকোয়েন্স হলো একটি পূর্ণসংখ্যার সেটের সাবসেট থেকে অন্য আরেকটি সেট S এর দিকে একটি ফাংশন। আমরা একটা সিকোয়েন্সকে {an} দিয়ে প্রকাশ করি যেখানে an হলো ধারার একটি টার্ম।
এবার যদি আমরা {an} কনসিডার করি, যেখানে an = 1/n, তাহলে ধারার টার্ম বা উপাদানগুলো শুরু হবে a1 থেকে এবং সেই উপাদানগুলোর লিস্ট হবে এরকম -
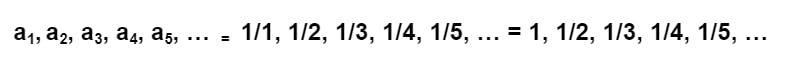
হ্যাশনোডে ম্যাথমেটিকাল টার্মগুলো লেখার কোনো ব্যবস্থা না থাকায় আমি doc ফাইলে লিখে এরপর তার স্ক্রিনসট এখানে দিচ্ছি যাতে আপনারা বুঝতে পারেন ভালভাবে।
Geometric Progression
Geometric progression হলো একটি সিকোয়েন্স যার ফর্মটা নিচের মতো হবে -
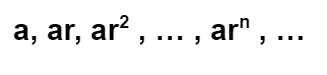
যেখানে initial term বা প্রথম উপাদান a এবং common ratio বা সাধারণ অনুপাত r উভয়ই বাস্তব সংখ্যা।

ধরি আমাদের কিছু সিকোয়েন্স আছে। সেগুলো হলো -

এগুলো সবগুলো geometric progression। আমরা যদি এক্সপোনেন্সিয়াল ফাংশনের সাথে এদের তুলনা করি এদের প্রথম উপাদান, a এবং সাধারণ অনুপাত, r বের করতে পারবো। প্রথমটার ক্ষেত্রে a = 1, r = -1; দ্বিতীয়টার ক্ষেত্রে a = 2, r = 5; তৃতীয়টার ক্ষেত্রে a = 6, r = 1/3। আমরা যদি n = 0 থেকে শুরু করি তাহলে ধারাগুলো দাঁড়াবে -

Arithmetic Progression
এটিও একটি সিকোয়েন্স যার ফর্মটা হবে এরকম - a, a + d, a + 2d, … , a + nd, …, যেখানে প্রথম উপাদান বা initial term হলো a এবং common difference বা সাধারণ অন্তর হলো d। এটা লিনিয়ার ফাংশন f(x) = a + dx এর অনুরূপ।
এবার আমরা একটা উদাহরণ দেখি। ধরি আমাদের কাছে দুইটা সিকোয়েন্স আছে যারা উভয়ই অ্যারিথমেটিক প্রগ্রেশন।

এবার এগুলোকে আমরা লিনিয়ার ফাংশনের সাথে তুলনা করে a এবং d বের করবো। প্রথমটাতে a = -1 এবং d = 4। দ্বিতীয়টাতে a =7, d = -3। তাহলে যদি আমরা n = 0 থেকে শুরু করি, ধারাগুলো দাঁড়াবে -
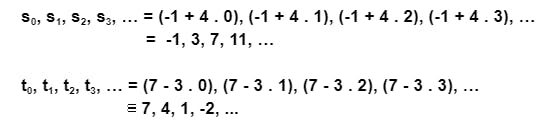
Sequences in Computer Science
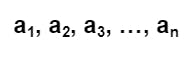
সিকোয়েন্সের এই ফর্মটা কম্পিউটার সায়েন্সে প্রায়ই ব্যবহৃত হয়। এই সিকোয়েন্সগুলোকে বলা হয় strings। স্ট্রিংকে লেখা হয় এভাবে -
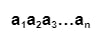
একটা স্ট্রিং এর length হলো যতটা টার্ম আছে সিকোয়েন্সের ততো। যদি কোনো স্ট্রিং এর কোনো টার্ম না থাকে তাহলে তার length হবে শূন্য, এবং একে বলা হবে empty string বা ফাঁকা স্ট্রিং। ফাঁকা স্ট্রিং কে সাধারণত λ (ল্যাম্বডা) দিয়ে প্রকাশ করা হয়।
উদাহরণস্বরূপ - স্ট্রিং abcd এর length হলো চার।
Recurrence Relation

Fibonacci Sequence

এই সিকোয়েন্স নিয়ে আমরা পরবর্তীতে আরো বিস্তারিত জানবো। আপাতত এটার কনসেপ্ট এখানে দিলাম।
Closed formula and Iteration
আমরা ইনিশিয়াল কন্ডিশনের সাথে একত্রে রিকারেন্স রিলেশন সলভ করতে পারি যদি আমরা একটা সুস্পষ্ট ফর্মুলা পাই। এই ফর্মুলাকে বলা হয় ক্লোজড ফর্মুলা।
অনেক মেথডের সাহায্যে আমরা রিকারেন্স রিলেশন সলভ করতে পারি। সেগুলো সম্পর্কে আমরা পরবর্তীতে জানবো। এই আর্টিকেলে আমরা ইটারেশন মেথড নিয়ে ধারণা নিবো।
আমরা রিকারেন্স রিলেশনের সাথে যে উদাহরণটা দেখেছিলাম সেটার রিকারেন্স রিলেশন এবং ইনিশিয়াল কন্ডিশন সলভ করবো এখন।

সিম্পল ক্যালকুলেশন। এখানে যেটা করলাম সেটা হলো ইটারেশন। আমরা রিকারেন্স রিলেশনকে ইটারেট করেছি। অর্থাৎ একটা প্রসেসকে বারবার পুনরাবৃত্তি করেছি। প্রথম যেটা করেছিলাম সেটাকে বলে forward substitution। এক্ষেত্রে ইনিশিয়াল কন্ডিশন দিয়ে শুরু করে an এ গিয়ে শেষ করেছিলাম। দ্বিতীয়টাকে বলে backward substitution। কারণ আমরা শেষ থেকে শুরু করে শুরুতে গিয়ে শেষ করেছিলাম। আমরা যখন ইটারেশন করবো, সাধারণত আমরা সিকোয়েন্সের অনুসারে একটা ফর্মুলা ধারণা করে নিই। আমাদের ধারণা সঠিক কিনা তার জন্য অবশ্যই আমাদের ম্যাথমেটিকাল ইন্ডাকশন অর্থাৎ গাণিতিকভাবে তা প্রতিষ্ঠা করতে হবে। সেটা আমরা পাঁচ নম্বর চাপটারে দেখবো। আট নম্বর চাপ্টারেও আমরা রিকারেন্স রিলেশন নিয়ে অনেক কিছু আলোচনা করবো।
এবার আমরা একটা বাস্তব উদাহরণ দেখি।
ধরি একজন লোক তার ব্যাংকে অ্যাকাউন্টে ১০,০০০ টাকা রাখলো। বার্ষিক ১১% সুদে ৩০ বছর পর তার অ্যাকাউন্টে কত টাকা জমা হবে?

Some Useful Special Integer Sequences
আমরা কিছু গুরুত্বপূর্ন সিকোয়েন্সের চার্ট দেখবো নিচে যা আমাদের পরবর্তীতে বিভিন্ন প্রব্লেম সলভ করতে কাজে দিবে -

Summations
এখন আমরা ধারার যোগফল কিভাবে বের করতে হয় তা শিখবো। তার জন্য আমাদেরকে আগে summation চিহ্নটার সাথে পরিচিত হতে হবে।

এখানে j কে বলা হয় সামেশনের ইনডেক্স (index of summation)। এখানে m, n এবং j ব্যবহার করতে হবে সেরকম কোনো কথা নেই। যেকোনো কিছু ব্যবহার করা যাবে। index of summation লোয়ার লিমিট m থেকে শুরু করে আপার লিমিট n পর্যন্ত যতো ইন্টিজার থাকবে সবগুলোর উপর অপারেশন চালাবে।
এবার আমরা কিছু সামেশনের উদাহরণ দেখি।


এবার আমরা একটা থিওরাম এবং তার প্রমাণ দেখবো। থিওরামটা হলো -
যদি a এবং b বাস্তব সংখ্যা হয় এবং r ≠ 0 হয়, তাহলে -
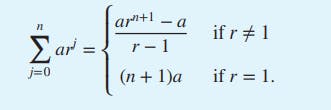

অনেক ক্ষেত্রে ডাবল সামেশনের প্রয়োজন পড়ে। সেরকম একটি উদাহরণ আমরা দেখবো এবার।
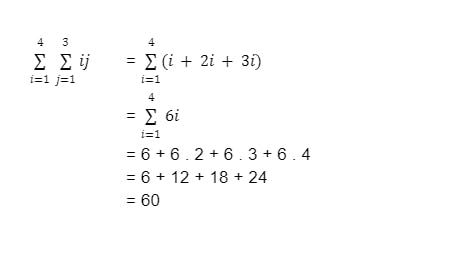
আমরা ফাংশনের জন্যও সামেশন করতে পারি। ধরি আমরা f(s) ফাংশনের যোগফল বের করবো S সেটের সকল মেম্বার s এর জন্য। এক্ষেত্রে নোটেশনটা হলো -
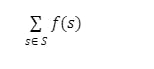
এবার আমরা একটি উদাহরণ দেখি -

আমি নিচে কিছু গুরুত্বপূর্ণ সামেশন ফর্মুলার চার্ট দিয়ে দিলাম।

Conclusion
ধারা এবং ধারার সমষ্টি নিয়ে আমরা আজ অনেক কিছু শিখলাম। পরবর্তীতে আমাদের প্রব্লেম সলভ করতে এগুলো কাজে দিবে। এরপরের আর্টিকেলে ম্যাট্রিক্স সম্পর্কে শিখবো।

