Introduction

অনেক ক্ষেত্রে আমরা একটি সেটের প্রতিটি উপদানকে অন্য একটি সেটের একটি নির্দিষ্ট উপাদানে অ্যাসাইন করি। একে ফাংশন বলা হয়। ডিসক্রিট ম্যাথের sequences বা ধারা এবং string বুঝার জন্য ফাংশন অনেক গুরুত্বপূর্ণ। একটা নির্দিষ্ট আকারের প্রবলেম সলভ করার জন্য কম্পিউটার সায়েন্সে ফাংশন ব্যবহৃত হয়। রিকারসিভ ফাংশন যেটার সাথে আমরা কমবেশি সবাই পরিচিত, তা কম্পিউটার সায়েন্সে ব্যাপকভাবে ব্যবহৃত হয়। এই আর্টিকেলে আমি ফাংশন নিয়ে বিস্তারিত আলোচনা করবো।

Function

ধরি A এবং B দুইটি পূর্ণ সেট। A থেকে B এর দিকে একটা ফাংশন f হলো A এর প্রতিটি উপাদানে B এর একটি নির্দিষ্ট উপাদান বরাদ্দ করা বা অ্যাসাইন করা। যদি ফাংশন f দ্বারা B এর নির্দিষ্ট উপাদান b কে A এর উপাদানে a তে অ্যাসাইন করা হয় তাহলে আমরা লিখতে পারি f(a) = b। যদি f, A থেকে B এর দিকে ফাংশন হয় তবে আমরা লিখতে পারি f : A -> B। জানি কথাগুলো বুঝতে কষ্ট হচ্ছে। একটা উদাহরণ দিই।

যেমন ধরি আমাদের কাছে একটা সেট আছে যেটা হলো ক্লাসের ডিসক্রিট ম্যাথের জন্য বরাদ্দ গ্রেডের সেট। সেটা হলো {A, B, C, D, F}। এবার আমরা ধরি রোল নাম্বার ১ পেলো A, ২ পেলো C, ৩ পেলো B, ৪ পেলো A এবং ৫ পেলো F। এই সিচুয়েশনকে আমরা নিচের মতো করে বুঝাতে পারি।

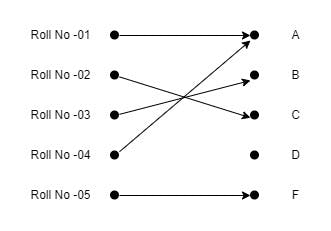
এটাই মূলত ফাংশনের একটা উদাহরণ। আমরা যদি গ্রেডের সেটকে B ধরি এবং রোল নাম্বারের সেটকে A ধরি তাহলে দেখতে পাচ্ছি B এর একটা নির্দিষ্ট উপাদান A এর প্রতিটি উপাদানে আমরা বরাদ্দ করেছি।

Relation

এই টার্মটা সংজ্ঞা দিয়ে বুঝানো অনেক কঠিন। সংজ্ঞা দিলে এরপর আপনারা এই আর্টিকেল আর পড়বেন না। তাই একটা উদাহরণ দিয়ে বুঝাই। ধরেন আমাদের কাছে দুইটা সেট আছে - A = {বাবা, মা, দাদা, দাদি, চাচা, মামা, খালা, ফুফু} এবং B = {আমি, ভাই, বোন, চাচাতো ভাই, চাচাতো বোন}। এবার বলা হলো দুইটা সেটের মধ্যে সম্পর্ক স্থাপন করতে যেন A এর উপাদানের সাথে B এর উপাদানের পিতামাতা এবং সন্তানের সম্পর্ক থাকে। তাহলে আমরা লিখতে পারি খুব সহজেই কোন কোন সম্পর্ক হতে পারে। আমরা নিচে সেগুলো এক এক করে লিখি।

• (বাবা, আমি)
• (বাবা, ভাই)
• (বাবা, বোন)
• (মা, আমি)
• (মা, ভাই)
• (মা, বোন)
• (চাচা, চাচাতো ভাই)
• (চাচা, চাচাতো বোন)

তাহলে আমাদের রিলেশন হবে একটা সেট যেখানে উপাদান হিসেবে থাকবে এই জোড়াগুলো অর্থাৎ রিলেশনকে যদি R হিসেবে আমরা ভাবি তাহলে R = {(বাবা, আমি), (বাবা, ভাই), (বাবা, বোন), (মা, আমি), (মা, ভাই), (মা, বোন), (চাচা, চাচাতো ভাই), (চাচা, চাচাতো বোন)}। আশা করি আপনারা রিলেশন কি বুঝেছেন।

প্রথম উদাহরণে আমাদেরকে যদি রিলেশন বের করতে বলে তাহলে আমরা প্রথমে আমাদের সেটগুলো কিভাবে হতে পারে সেটা লিখি - A = {Roll-01, Roll-02, Roll-03, Roll-04, Roll-05}, B = {A, B, C, D, F}। আমাদের শর্ত অনুসারে রিলেশন হবে R = {(Roll-01, A), (Roll-02, C), (Roll-03, B), (Roll-04, A), (Roll-05, F)}। আশা করি ক্লিয়ার হয়ে গেছে ফাংশনের কনসেপ্ট।

মজার ব্যাপার হলো রিলেশন থেকে আমরা ফাংশন লিখতে পারি। যেমন এই রিলেশন থেকে আমরা লিখতে পারি f(Roll-01) = A, f(Roll-02) = C, f(Roll-03) = B, f(Roll-04) = A, f(Roll-05) = F।

রিলেশনকে বাংলায় অন্বয় বলা হয়ে থাকে।

Domain, Codomain and Range

• Domain - যদি A থেকে B তে একটা ফাংশন f হয় তবে A হচ্ছে f এর ডোমেইন। যেমন উপরের উদাহরণে ডোমেইন হচ্ছে {Roll-01, Roll-02, Roll-03, Roll-04, Roll-05}।
• Codomain - যদি A থেকে B তে একটা ফাংশন f হয় তবে B হচ্ছে f এর কোডোমেইন। উপরের উদাহরণে কোডোমেইন হচ্ছে {A, B, C, D, F}
• Range - যদি f(a) = b হয় তাহলে আমরা b কে a এর রেঞ্জ বলতে পারি। অর্থাৎ B এর যে উপাদানগুলো A এর উপাদানে বরাদ্দ হয় তাদেরকে রেঞ্জ বলে। উপরের উদাহরণে রেঞ্জ হচ্ছে {A, B, C, F}

Some examples of functions

এবার যা যা শিখলাম সব একত্র করে একটা উদাহরণ দেখি।

• উদাহরণ - ১ - আমাদের কাছে একটা রিলেশন আছে R = { (Abdul, 22), (Nayem, 24), (Jahid, 21), (Aditya, 22), (Shovon, 24), (Arpita, 22)}। এখানে প্রতিটা জোড়ার প্রথম উপাদান হচ্ছে একজনের নাম এবং দ্বিতীয় উপাদান হচ্ছে তার বয়স। প্রথম কাজ হচ্ছে এখান থেকে ফাংশন বের করা। দ্বিতীয় কাজ হচ্ছে ফাংশনের ডোমেইন এবং রেঞ্জ বের করা।

  • আমাদের ফাংশন যদি f হয় তাহলে এই রিলেশন থেকে আমরা লিখতে পারি f(Abdul) = 22, f(Nayem) = 24, f(Jahid) = 21, f(Aditya) = 22, f(Shovon) = 24 এবং f(Arpita) = 22। ডোমেইন হবে {Abdul, Nayem, Jahid, Aditya, Shovon, Arpita}, রেঞ্জ হলো {21, 22, 24}।

• উদাহরণ - ২ - ধরি f : Z → Z ফাংশনটি একটা পূর্ণসংখ্যার মধ্যে ঐ পূর্ণসংখ্যার বর্গকে অ্যাসাইন করেছে। অর্থাৎ f(x) = x², যেখানে ডোমেইন হলো সকল পূর্ণসংখ্যার সেট এবং রেঞ্জ হলো সকল পূর্ণ বর্গের সেট অর্থাৎ {0, 1, 4, 9, ...}।

Addition and Multiplications of functions

যদি একটা ফাংশনের কোডোমেইন বাস্তব সংখ্যার সেট হয় তাহলে তাহলে একে বলা হয় real-valued, আর যদি পূর্ণসংখ্যার সেট হয় তবে বলা হয় integer-valued। একই ডোমেইনের দুইটি রিয়েল-ভ্যালুড বা দুইটি ইন্টিজার-ভ্যালুড ফাংশন পরস্পর যোগ এবং গুণ করা যায়।

যদি f1 এবং f2, A থেকে R এ ফাংশন হয় তবে f1 + f2 এবং f1f2 ও A থেকে R এ ফাংশন হবে।

(f1 + f2)(x) = f1(x) + f2(x) (f1f2)(x) = f1(x)f2(x)

• উদাহরণ - ১ - যদি R to R ফাংশন f1 এবং f2 হয় যেন f1(x) = x² এবং f2(x) = x - x² হয়, তবে f1 + f2 এবং f1f2 কি হবে?

  • (f1 + f2)(x) = f1(x) + f2(x) = x² + x - x² = x
  • (f1f2)(x) = f1(x)f2(x) = x²(x - x²) = x^3 - x^4

Another Basic Concept

যদি A থেকে B তে ফাংশন f হয় এবং S, A এর একটি সাবসেট হয়, তবে ঐ ফাংশনের অধীনে S এর রেঞ্জ হবে S এর উপাদানগুলোর রেঞ্জ থেকে গঠিত হওয়া B এর সাবসেট। যাকে আমরা লিখতে পারি -

f(S) = {f(s) | s ∈ S}

সব মাথার উপর দিয়ে গেছে বুঝেছি। উদাহরণ দিই একটা। তাহলেই ক্লিয়ার হয়ে যাবে।

ধরি A = {a, b, c, d, e} এবং B = {1, 2, 3, 4}। f(a) = 2, f(b) = 1, f(c) = 4, f(d) = 1, এবং f(e) = 1। সাবসেট S = {b, c, d}। তাহলে S এর রেঞ্জ হবে f(S) = {1, 4}। আশা করি এবার আপনারা বুঝতে পেরেছেন।

One-to-One functions

ফাংশন f কে one-to-one বলা হবে, যদি ও কেবল যদি f(a) = f(b), f এর ডোমেইনের মধ্যে থাকা সকল a ও b এর জন্য a = b প্রকাশ করে। যদি একটা ফাংশন one-to-one হয় তাহলে একে injective ফাংশন বলা হবে।

অর্থাৎ এখানে কিছু ফাংশন কখনও দুইটা ভিন্ন ডোমেইনের উপাদানের মধ্যে একই ভ্যালু অ্যাসাইন করে না। এটাই one-to-one। একটা উদাহরণ দিলে ক্লিয়ার হয়ে যাবে ব্যাপারটা।

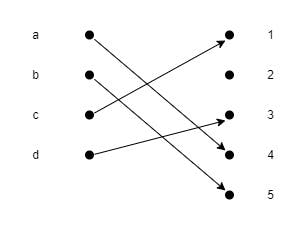
ধরি A = {a, b, c, d} এবং B = {1, 2, 3, 4, 5}। f(a) = 4, f(b) = 5, f(c) = 1 এবং f(d) = 3। আমাদের দেখাতে হবে f ফাংশন one-to-one কিনা।

এখানে আমরা দেখতে পাচ্ছি ডোমেইনের প্রতিটা উপাদান আলাদা আলাদা ভ্যালু গ্রহণ করেছে। দুইটা উপাদান একই ভ্যালু গ্রহণ করেনি। তাই এই ফাংশন one-to-one।

Onto Functions

বইয়ের ভাষায় যদি বলি তাহলে তা হলো -

A function f from A to B is called onto, or a surjection, if and only if for every element b ∈ B there is an element a ∈ A with f(a) = b. A function f is called surjective if it is onto.

অর্থাৎ B এর প্রতিটি উপাদানের জন্য অন্তত A এর একটা উপাদান থাকবে। এতক্ষণ পর্যন্ত আমরা যা দেখেছি সেখানে B এর কোনো কোনো উপাদান খালি পড়ে ছিল। কিন্তু onto ফাংশনের ক্ষেত্রে সেটা হবে না। আমরা নিচের ফিগারটা দেখলে বুঝতে পারবো।

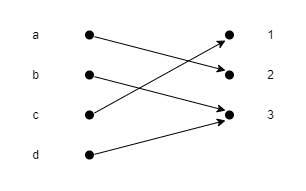
আমরা যদি one-to-one এর উদাহরণটা ধরি তাহলে সেটা onto না, কারণ সেখানে B এর 2 উপাদান অব্যবহৃত ছিল।

One-to-one correspondence or bijection

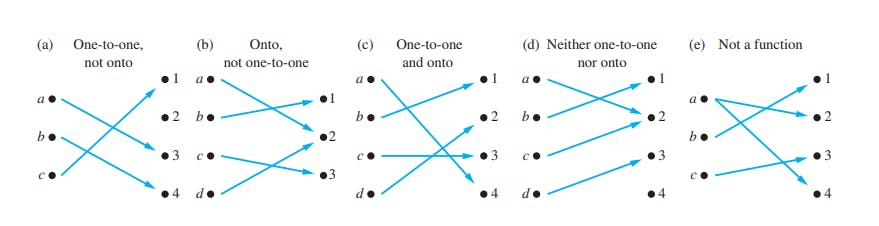
একটা ফাংশন যদি one-to-one এবং onto উভয়ই হয়, তবে সেই ফাংশনকে আমরা One-to-one correspondence or bijection বলতে পারি। নিচের ফিগারের মাধ্যমে এটি বুঝানো হলো।

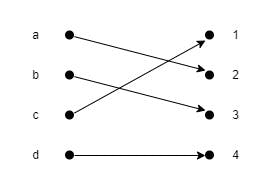
নিচে কিছু ডিফারেন্ট করেসপন্ডেন্স দেয়া হলো।

Inverse Functions

ধরি f হলো A থেকে B তে একটা one-to-one correspondence। f এর ইনভার্স ফাংশন হলো একটি ফাংশন যা A এর একটি নির্দিষ্ট উপাদান a কে B এর উপাদান b তে অ্যাসাইন করে। অর্থাৎ ফাংশনের সংজ্ঞার উলটো। f এর ইনভার্স ফাংশনকে কে f^-1 দিয়ে প্রকাশ করা হয়। যখন f(a) = b হবে, তখন f^-1(b) = a হবে।

একটা ফাংশনের ইনভার্স থাকবে যদি ও কেবল ঐ ফাংশন one-to-one এবং onto উভয়ই হয় অর্থাৎ one-to-one correspondence হয়। যদি one-to-one correspondence না হয় তাহলে ঐ ফাংশনের ইনভার্স থাকবে না।

Composition of functions

যদি g, A থেকে B তে একটা ফাংশন হয় এবং f, B থেকে C তে একটা ফাংশন হয় তবে A থেকে C তে ফাংশনকে প্রকাশ করা হয় fog দিয়ে। যেখানে fog = f(g(a))। এটাকে বলা হয় composition of functions।

ধরি তিনটা সেট আছে A = {a, b, c}, B = {a, b, c} এবং C = {1, 2, 3}। g হলো A থেকে B তে একটা ফাংশন যেখানে g(a) = b, g(b) = c, এবং g(c) = a। আবার f হলো B থেকে C তে ফাংশন যেখানে f(a) = 3, f(b) = 2, এবং f(c) = 1। fog এবং gof কি হবে?

প্রথমে আমরা fog বের করি।

• fog(a) = f(g(a)) = f(b) = 2
• fog(b) = f(g(b)) = f(c) = 1
• fog(c) = f(g(c)) = f(a) = 3

এরপর আমরা বের করবো gof। কিন্তু তা করা যাবে না। কারণ gof(a) = g(f(a)) = g(2)। কিন্তু আমাদের g(2) এর জন্য কিছু বলা নেই। তাই gof বের করা যাবে না।

Graph of a function

একটা ফাংশন f এর গ্রাফ হলো ordered pairs এর সেট। অর্থাৎ {(a, b) ∣ a ∈ A and f(a) = b}। এই জোড়াগুলোকে গ্রাফে বসিয়ে দিলেই এই ফাংশনের গ্রাফ পাওয়া যাবে। একটা উদাহরণ দেয়ার চেষ্টা করছি আমি।

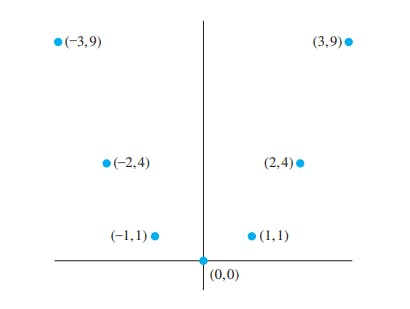
একটা পূর্ণসংখ্যার সেট থেকে আরেকটি পূর্ণসংখ্যার সেটের ফাংশন f(x) = x² হলে এর গ্রাগ হবে (x, f(x)) = (x, x²), যেখানে x হলো একটি পূর্ণসংখ্যা। এর গ্রাফটা নিচে দেখানো হলো। ধরি আমরা x এর মান -3, -2, -1, 0, 1, 2, 3 নিলাম। তাহলে জোড়াগুলো হবে (-3, 9), (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4), (3, 9) এরকম। তাহলে গ্রাফটা হবে -

Conclusion

এই গেলো মোটামুটি ফাংশন নিয়ে ধারণা। পরের আর্টিকেলে আমরা sequences and summations (ধারা ও সমষ্টি) নিয়ে আলোচনা করবো।