Introduction

একটু ভাবুন যদি আমাদের ডিকশনারি alphabetically sorted না হতো, আমাদের স্কুলের হাজিরা খাতায় যদি আমাদের রোল নাম্বার সিরিয়ালি না থাকতো, বা আমাদের কন্টাক্ট লিস্ট যদি সর্টেড না হতো কি হতো? ভাবতে পারছেন না, তাই তো? কিছু খুঁজতে গেলে দিন চলে যেতো। সর্টিং আমাদের জীবনকে অনেক সহজ করে দিয়েছে। কেউ যদি আমাদেরকে অবিন্যস্ত বা unsorted একটা লিস্ট দেয় সেটাকে আমরা সর্ট করার জন্য যে অ্যালগরিদম ব্যবহার করি সেটাকে বলে সর্টিং অ্যালগরিদম। এখন প্রায় ১০০টার উপর সর্টিং অ্যালগরিদম আছে। প্রতিনিয়ত নতুন নতুন অ্যালগরিদম তৈরি হচ্ছে। কোনোটা খুব সহজে ইমপ্লিমেন্ট করা যায়, কোনোটা খুব এফিসিয়েন্ট, কোনোটা আবার কম্পিউটার আর্কিটেকচার থেকে সুবিধা নিতে পারে।

এই আর্টিকেলে আমরা আলোচনা করবো নিচের সর্টিং অ্যালগরিদমগুলো নিয়ে।

• Bubble sort
• Insertion sort
• Selection sort
• Binary insertion sort
• Shaker sort / Bidirectional bubble sort

এগুলো মোটামুটি আমাদের প্রাত্যহিক কাজে লাগে। এগুলো ছাড়াও আরো কিছু অ্যালগরিদম আছে যা আমাদের প্রতিনিয়ত কাজে লাগে। সেগুলো হলো -

• Merge sort
• Quick sort
• Tournament sort

Merge এবং Quick সর্ট বুঝতে হলে আমাদের রিকারশন সম্পর্কে জানতে হবে আগে। আমরা যখন রিকারশন নিয়ে আলোচনা করবো তখন এই দুইটা অ্যালগরিদম নিয়ে সেখানে আলোচনা করবো। Tournament সর্ট বুঝতে হলে আমাদের বাইনারি ট্রী সম্পর্কে জানতে হবে। এই অ্যালগরিদম আমরা যখন বাইনারি ট্রী নিয়ে আলোচনা করবো তখন শিখবো।

প্রতিটার লিংক আমি এখানে আপডেট করে দিবো যখন আলোচনা করবো।

Bubble sort

বাবল সর্ট হলো সবচেয়ে সিম্পল সর্টিং অ্যালগরিদমগুলোর মধ্যে অন্যতম একটি অ্যালগরিদম। তবে এটি খুব এফিসিয়েন্ট না। বাবল সর্ট একটা লিস্টের প্রতিটা উপাদানকে তার ঠিক পরবর্তী উপাদানের সাথে তুলনা করে দেখবে সেটা ইনক্রিজিং অর্ডারে আছে কিনে। যদি থাকে তো ভাল। আর না থাকলে এই দুইটা উপাদান পরস্পরের সাথে ইন্টারচেইঞ্জ করবে। এভাবে চলতে থাকবে যতক্ষণ পর্যন্ত সর্ট করা শেষ হবে না। আমরা যদি লিস্টের ছোট উপাদানগুলোকে হালকা বস্তু বা বাবলের সাথে তুলনা করি তাহলে সব উপাদানকে যদি একটা পানিভর্তি ট্যাংকে ফেলি তাহলে সবচেয়ে হালকা বস্তু অর্থাৎ বাবল উপরে উঠে আসবে এবং সবচেয়ে ভারী বস্তু নিচে চলে যাবে। বাকিগুলো ভর অনুযায়ী সিরিয়ালি বিন্যস্ত হয়ে যাবে। চলুন একটা উদাহরণ দেখা যাক।

আমরা বাবল সর্ট ব্যবহার করে ৩, ২, ৪, ১, ৫ এই লিস্টকে ছোট থেকে বড় এই সিকোয়েন্সে সাজাবো।

প্রথমে আমরা প্রথম দুইটা উপাদান ৩ এবং ২ কে নিয়ে তুলনা করবো। যেহেতু ৩ > ২, সেহেতু ৩ ও ২ পরস্পর জায়গা ইন্টারচেইঞ্জ করবে। এরা জায়গা অদলবদল করার পর আমাদের লিস্ট দাঁড়াবে ২, ৩, ৪, ১, ৫। এরপর ৩ ও ৪ কে কম্পেয়ার করবো। দেখা যাচ্ছে ৩ < ৪, সুতরাং এরা যার যার জায়গায় থেকে যাবে। এরপর ৪ ও ১ এর মধ্যে ৪ > ১, সুতরাং এরা জায়গা অদলবদল করবে। লিস্ট দাঁড়াবে ২, ৩, ১, ৪, ৫। এরপর ৪ ও ৫ এর মধ্যে ৪ < ৫, সুতরাং এরা যার যার জায়গায় থেকে যাবে। এরই সাথে আমাদের প্রথম পাস শেষ।

দ্বিতীয় পাসে ২ এবং ৩ কে তুলনা করে দেখা যাচ্ছে ২ < ৩। সুতরাং এরা এদের জায়গাতেই থাকবে। এরপর ৩ ও ১ এর ক্ষেত্রে ৩ < ১, সুতরাং এরা জায়গা অদলবদল করবে। তাহলে লিস্ট দাঁড়াবে ২, ১, ৩, ৪, ৫। এরপর ৩, ৪, ৫ এদের নিজেদের জায়গাতেই থাকবে কারণ ৩ < ৪ এবং ৪ < ৫। আমাদের দ্বিতীয় পাসও শেষ।

তৃতীয় পাসে আমরা প্রথমে ২ ও ১ এর মধ্যে তুলনা করবো। দেখা যাচ্ছে ২ > ১। সুতরাং এরা ইন্টারচেইঞ্জ করবে জায়গা। তাহলে লিস্ট দাঁড়াবে ১, ২, ৩, ৪, ৫। এরপরের জোড়াগুলোর ক্ষেত্রে ২ < ৩, ৩ < ৪ এবং ৪ < ৫। সুতরাং এরা যে যার জায়গায় থেকে যাবে। আমাদের তৃতীয় পাস শেষ। সেই সাথে আমাদের বাবল সর্টও শেষ। আমাদের সর্টেড লিস্ট তাহলে দাঁড়ালো ১, ২, ৩, ৪, ৫।

এই স্টেপগুলোকে নিচের ডায়গ্রামের মাধ্যমে আরো সুন্দরভাবে বুঝতে পারবেন।

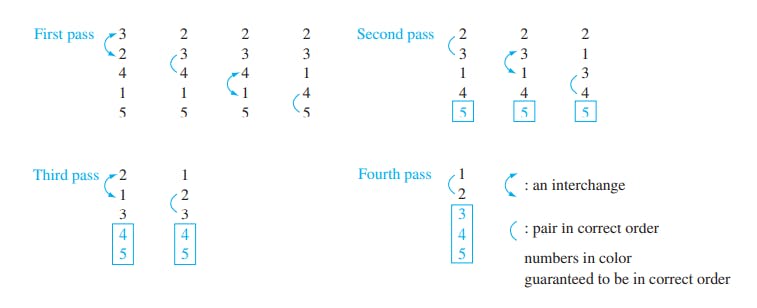
image courtesy: Discrete Mathematics and its application by Kenneth Rosen

এবার আমরা বাবল সর্টের সুডোকোড কিরকম হতে পারে সেটা একটু দেখবো।

procedure bubble sort(a1,… , an : real numbers with n ≥ 2)
for i := 1 to n − 1
    for j := 1 to n − i
        if aj > aj+1 then interchange aj and aj+1
{a1,… , an is in increasing order}

Insertion sort

এটাও খুবই সিম্পল একটা অ্যালগরিদম। এটা বাবল সর্টের চেয়ে এফিসিয়েন্ট তবে মোস্ট এফিসিয়েন্ট না। এখানে একটা লিস্ট সর্ট করার জন্য লিস্টের দ্বিতীয় উপাদান থেকে সর্টিং শুরু করা হয়। দ্বিতীয় উপাদানকে প্রথম উপাদানের সাথে কম্পেয়ার করা হয়। যদি দ্বিতীয় উপাদান > প্রথম উপাদান হয় তাহলে দ্বিতীয় উপাদান প্রথম পজিশনে চলে আসবে। আর যদি দ্বিতীয় উপাদান < প্রথম উপাদান হয় তাহলে যে যার যার জায়গায় থাকবে। এরপর তৃতীয় উপাদান আবার প্রথম উপাদানের সাথে কম্পেয়ার করে যদি দেখে এরা সর্টেড না, তাহলে জায়গা অদলবদল করবে। এভাবে চলতে থাকবে সর্ট শেষ না হওয়া পর্যন্ত। আমরা উপরের উদাহরণটা দিয়ে বুঝার চেষ্টা করি। আমাদের লিস্ট ছিল ৩, ২, ৪, ১, ৫।

প্রথমে দ্বিতীয় উপাদান ২ এর সাথে প্রথম উপাদান কম্পেয়ার করবো আমরা। দেখা যাচ্ছে ৩ > ২। সুতরাং ২ প্রথম পজিশনে যাবে এবং ৩ দ্বিতীয় পজিশনে চলে আসবে। তাহলে লিস্ট দাঁড়াবে ২, ৩, ৪, ১, ৫। এখানে ২ এবং ৩ কিন্তু সর্টেড। এবার তৃতীয় উপাদান ৪ এর সাথে প্রথম উপাদান ২ এর তুলনা করবো আমরা। দেখা যাচ্ছে ২ < ৪। সুতরাং জায়গা চেইঞ্জ করা লাগবে না। এরপর চতুর্থ উপাদান ১ এর সাথে ২ এর তুলনা করে দেখা যাচ্ছে ২ > ১। সুতরাং ১ প্রথম পজিশনে চলে যাবে এবং বাকি উপাদানগুলো এক ঘর করে সরে যাবে। তাহলে লিস্ট দাঁড়ালো ১, ২, ৩, ৪, ৫। সবশেষে ৫ কে কম্পেয়ার করলে দেখবো সে ঠিক জায়গাতেই আছে। সুতরাং আমাদের ইনসারশন সর্টিং কমপ্লিটেড।

এবার আমরা সুডোকোড দেখবো।

procedure insertion sort(a1, a2,… , an: real numbers with n ≥ 2)
for j := 2 to n
    i := 1
    while aj > ai
        i := i + 1
    m := aj
    for k := 0 to j − i − 1
        aj−k := aj−k−1
    ai := m
{a1,… , an is in increasing order}

Selection Sort

সিলেকশন সর্টে মূলত লিস্টের সবচেয়ে ছোট উপাদান কোনটা সেটা বের করা হয়। সেটা বের করে সেই উপাদানকে ১ম পজিশনের সাথে ইন্টারচেইঞ্জ করা হয়। ১ম পজিশন ফিক্সড। ওটাতে আর হাত দেয়া যাবে না। এরপর বাকি উপাদানগুলোর মধ্যে সবচেয়ে ছোট উপাদান বের করে দ্বিতীয় পজিশনের সাথে ইন্টারচেইঞ্জ করা হয়। এভাবে করে চলতে থাকবে যতক্ষণ না লিস্ট সর্টেড হয়।

আমাদের উদাহরণে লিস্ট ছিল ৩, ২, ৪, ১, ৫। এখানে সবচেয়ে ছোট উপাদান হলো ১। একে প্রথম পজিশনের সাথে ইন্টারচেইঞ্জ করলে লিস্ট হবে ১, ২, ৪, ৩, ৫। এরপরের ছোট সংখ্যা হলো ২। সেটা দ্বিতীয় পজিশনেই আছে। এরপরের ছোট সংখ্যা ৩। একে তৃতীয় পজিশনের সাথে ইন্টারচেইঞ্জ করলে দাঁড়াবে ১, ২, ৩, ৪, ৫। এরপরের ছোট সংখ্যাগুলো যথাক্রমে ৪ ও ৫ চতুর্থ ও পঞ্চম পজিশনে আছে। সুতরাং আমাদের সর্টেড লিস্ট হলো ১, ২, ৩, ৪, ৫।

এবার আমরা সুডোকোডটা লিখে ফেলি।

procedure insertion sort(a1,… , an : real numbers with n ≥ 2)
i := 1{i is left endpoint of search interval}
j := n {j is right endpoint of search interval}
while i < j
    m := [(i + j) ∕ 2]
    if x > am then i := m + 1
    else j := m
if x < ai then location := i
else location := i + 1
{a1,… , an is in increasing order}

Binary Insertion Sort

বাইনারি ইনসার্শন সর্ট এবং ইনসার্শন সর্টের মধ্যে পার্থক্য হলো ইনসার্শন সর্টে লিনিয়ার সার্চ ব্যবহার করা হয় এবং বাইনারি ইনসার্শন সর্টে বাইনারি সার্চ ব্যবহার করা হয়।

আমরা চাইছি বাইনারি ইনসার্শন সর্ট ব্যবহার করে ৩, ২, ৪, ৫, ১, ৬ এই লিস্টকে সর্ট করতে। তাহলে আমরা প্রথমে ২ এর পজিশন বের করবো। ২ কে ৩ এর সাথে তুলনা করলে আমরা পাবো ২ < ৩। সুতরাং ২ প্রথমে চলে আসবে। বাকিসব এক ঘর করে পিছনে গিয়ে দাঁড়াবে ২, ৩, ৪, ৫, ১, ৬। এরপর আমরা ৪ এর পজিশন বের করবো। ৪ এর আগে আছে দুইটা সংখ্যা। ২, ৩। এই ২, ৩ এর লিস্টকে যদি বাইনারি সার্চের মাধ্যমে করি তাহলে ২ এবং ৩ দুইটা লিস্টে ভাগ হবে। ৪ কে ২ এর সাথে তুলনা করে পাচ্ছি ২ < ৪ এবং ৩ এর সাথে তুলনা করে পাচ্ছি ৩ < ৪। সুতরাং ৪ তার জায়গাতেই থেকে যাবে এবং লিস্ট হবে ২, ৩, ৪, ৫, ১, ৬। এরপর ৫ এর পজিশন বের করার জন্য আমাদের হাতে আছে ২, ৩, ৪ এই লিস্ট। একে দুই ভাগে ভাগ করে আমরা পাচ্ছি ২, ৩ এর একটা লিস্ট এবং অন্য ভাগে পাচ্ছি ৪। প্রথম লিস্টের শেষ উপাদান ৩ এর সাথে ৫ কে তুলনা করলে পাচ্ছি ৩ < ৫। সুতরাং ঐ লিস্ট বাদ। এরপর ৪ এর সাথে তুলনা করলে পাচ্ছি ৪ < ৫। সুতরাং ৫ তার জায়গাতেই থাকবে। এরপর ১ এর পজিশন বের করবো আমরা। ১ আগে আমরা পাচ্ছি ২, ৩, ৪, ৫। দুই ভাগ করলে পাচ্ছি ২, ৩ এবং ৪, ৫। প্রথম লিস্টের শেষ উপাদান ৩ এর সাথে তুলনা করলে পাচ্ছি ৩ > ১। সুতরাং আমরা ৩ এর আগের সংখ্যা অর্থাৎ ২ এর সাথে তুলনা করবো। তুলনা করে পেলাম ২ > ১। সুতরাং ১, ২ এর আগে বসে যাবে। তাহলে লিস্ট দাঁড়াবে ১, ২, ৩, ৪, ৫, ৬। ৬ কে আমরা একই ভাবে কম্পেয়ার করবো। করে সবশেষে আমাদের সর্টেড লিস্ট দাঁড়াবে ১, ২, ৩, ৪, ৫, ৬।

জানি হয়তো মাথা ঘুরাচ্ছে। ছোট করে প্রসিডিউরটা বুঝিয়ে দিই। যে সংখ্যাকে সর্ট করতে চাইবেন আপনি সেই সংখ্যার আগে যত সংখ্যা থাকবে সেগুলোর উপর বাইনারি সার্চ করবেন। এটাই মাথায় রাখবেন।

এবার সুডোকোড দেখবো আমরা।

. procedure binary insertion sort(a1, a2,… , an: real numbers with n ≥ 2)
for j := 2 to n
    {binary search for insertion location i}
    left := 1
    right := j − 1
    while left < right
        middle := [(left + right)∕2]
        if aj > amiddle then left := middle + 1
        else right := middle
if aj < aleft then i := left else i := left + 1
{insert aj in location i by moving ai through aj−1 toward back of list}
m := aj
for k := 0 to j − i − 1
    aj−k := aj−k−1
ai := m
{a1, a2,… , an are sorted}

Shaker Sort / Bidirectional bubble sort

একে Cocktail sort ও বলা হয়। এটা মূলত বাবল সর্ট। তবে বাবল সর্টে চেক করা হয় শুরু থেকে শেষের দিকে। কিন্তু এখানে শুরু থেকে শেষের দিকে একবার সর্ট করা হয় এবং শেষ থেকে শুরুর দিকে আবার সর্ট করা হয়। এভাবে চলতে থাকবে যতক্ষণ না আর জায়গা এক্সচেইঞ্জ করার কিছু থাকবে না।

ধরেন আমরা ৩, ৫, ১, ৪, ৬, ২ এই লিস্টকে সর্ট করতে চাইছি। শেকার সর্টে প্রথম পাসের ইটারেশন নিচে দেয়া হলো।

• (৩, ৫, ১, ৪, ৬, ২) => (৩, ৫, ১, ৪, ৬, ২)
• (৩, ৫, ১, ৪, ৬, ২) => (৩, ১, ৫, ৪, ৬, ২) (যেহেতু ৫ > ১)
• (৩, ১, ৫, ৪, ৬, ২) => (৩, ১, ৪, ৫, ৬, ২) (যেহেতু ৫ > ৪)
• (৩, ১, ৪, ৫, ৬, ২) => (৩, ১, ৪, ৫, ৬, ২)
• (৩, ১, ৪, ৫, ৬, ২) => (৩, ১, ৪, ৫, ২, ৬) (যেহেতু ৬ > ২)

এবার দ্বিতীয় পাসে আমরা শেষ থেকে শুরু করবো।

• (৩, ১, ৪, ৫, ২, ৬) => (৩, ১, ৪, ৫, ২, ৬)
• (৩, ১, ৪, ৫, ২, ৬) => (৩, ১, ৪, ২, ৫, ৬) (যেহেতু ২ < ৫)
• (৩, ১, ৪, ২, ৫, ৬) => (৩, ১, ২, ৪, ৫, ৬) (যেহেতু ২ < ৪)
• (৩, ১, ২, ৪, ৫, ৬) => (৩, ১, ২, ৪, ৫, ৬)
• (৩, ১, ২, ৪, ৫, ৬) => (১, ৩, ২, ৪, ৫, ৬) (যেহেতু ১ < ৩)

তৃতীয় পাসে আমরা শুরু করবো আবার প্রথম থেকে।

• (১, ৩, ২, ৪, ৫, ৬) => (১, ৩, ২, ৪, ৫, ৬)
• (১, ৩, ২, ৪, ৫, ৬) => (১, ২, ৩, ৪, ৫, ৬) ( যেহেতু ২ < ৩)
• (১, ২, ৩, ৪, ৫, ৬) => (১, ২, ৩, ৪, ৫, ৬)
• (১, ২, ৩, ৪, ৫, ৬) => (১, ২, ৩, ৪, ৫, ৬)
• (১, ২, ৩, ৪, ৫, ৬) => (১, ২, ৩, ৪, ৫, ৬)

আমাদের লিস্ট সর্টেড।

এবার সুডোকোডটাও লিখে ফেলি আমরা।

procedure shakersort(a1, . . . , an)
front := 1
back := n
still interchanging := true
while front < back and still interchanging
    if n + back + front is odd then {process from front to back}
        still interchanging := false
        for j := front to back − 1
            if aj > aj+1 then
                still interchanging := true
                interchange aj and aj+1
        back := back − 1
  else {process from back to front}
        still interchanging := false
        for j := back down to front + 1
            if aj−1 > aj then
                still interchanging := true
                interchange aj−1 and aj
        front := front + 1
{ a1, . . . , an is in nondecreasing order}