Introduction
দুই বা ততোধিক সেটকে বিভিন্ন উপায়ে আমরা কম্বাইন্ড বা একত্র করতে পারি। যেমন ধরি আমাদের কাছে দুইটা সেট আছে। প্রথম সেটটি ধরলাম যারা উচ্চতর গণিত ঐচ্ছিক বিষয় হিসেবে নিয়েছে এবং দ্বিতীয় সেটটি হলো যারা জীববিজ্ঞান ঐচ্ছিক বিষয় হিসেবে নিয়েছে। আমরা চাইলে কতজন উচ্চতর গণিত অথবা জীববিজ্ঞান ঐচ্ছিক হিসেবে নিয়েছে তার সেট তৈরি করতে পারি, কতজন এই দুইটা বিষয় ঐচ্ছিক হিসেবে নিয়েছে সেটার সেট তৈরি করতে পারি, কতজন জীববিজ্ঞান নেয়নি তার সেট তৈরি করতে পারি। এভাবে অনেককিছুই আমরা করতে পারি। এই আর্টিকেলে আমরা দেখবো কি কি উপায়ে সেটের অপারেশন করা যায়। চলুন শুরু করা যাক।
Union of sets
আমরা নাইন টেনে থাকতে আমাদেরকে বুঝানো হয়েছিলো ইউনিয়ন মানে দুইটা সেটের কমন, আনকমন সকল উপাদান নিয়ে একটি নতুন সেট তৈরি হবে। অর্থাৎ যদি আমরা দুইটা সেট নিই A এবং B, তাহলে এই দুই সেটের ইউনিয়ন হবে এমন একটি সেট যার মধ্যে A, B এর মধ্যে যা আছে সব থাকবে। তবে যদি কোনো উপাদান দুইটি সেটের মধ্যেই থাকে বা একাধিকবার থাকে একটা সেটে, তাহলে আমরা ঐ উপাদান শুধুমাত্র একবারই নিবো আমাদের ইউনিয়নের মধ্যে। ইউনিয়নকে প্রকাশ করা হয় ∪ চিহ্ন দিয়ে, এবং দুইটা সেটের ইউনিয়ন বুঝাতে লেখা হয় A ∪ B।
একটা উপাদান x, A এবং B এর ইউনিয়নের উপাদান হবে যদি ও কেবল যদি x ∈ A অথবা x ∈ B হয়। অর্থাৎ x যদি A অথবা B এর সদস্য হয় তবেই তা A এবং B এর ইউনিয়নের সদস্য হবে। এটাকে আমরা যদি গাণিতিক বিবৃতিতে প্রকাশ করি তাহলে লেখা যায় -
A ∪ B = {x ∣ x ∈ A ∨ x ∈ B}
নিচের ভেন ডায়গ্রাম দিয়ে এই সংজ্ঞাটি বুঝানোর চেষ্টা করা হলো।

এখানে হাইলাইট করা অংশ পুরোটাই ইউনিয়ন বুঝানো হচ্ছে।
উদাহরণ - A = {1, 3, 5} and B = {1, 2, 3}. তাহলে A ∪ B = {1, 3, 5} ∪ {1, 2, 3} = {1, 2, 3, 5} হবে।
Intersections of sets
এক্ষেত্রে শুধু যে সকল উপাদান A এবং B উভয় সেটের মধ্যে আছে সেগুলো নিয়েই ইন্টারসেকশন সেট তৈরি হবে। একে প্রকাশ করা হয় ∩ দিয়ে এবং দুইটা সেটের ইন্টারসেকশন বুঝানো হয় A ∩ B লিখে।
একটা উপাদান x, A ∩ B এর সদস্য হবে যদি ও কেবল যদি x ∈ A এবং x ∈ B হয়। অর্থাৎ যদি
A ∩ B = {x ∣ x ∈ A ∧ x ∈ B}
হয়। নিচের ভেন ডায়গ্রামের মাধ্যমে এটি বুঝানো হলো।
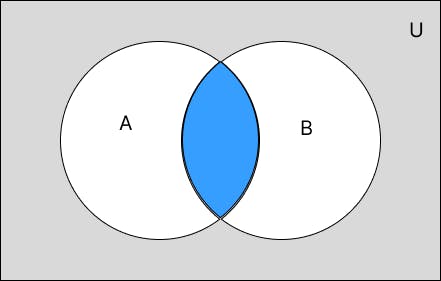
উদাহরণ - যদি A = {1, 3, 5} এবং B = {1, 2, 3} হয় তবে A ∩ B = {1, 3, 5} ∩ {1, 2, 3} = {1, 3} হবে।
Disjoint
যদি দুইটা সেটের ইন্টারসেকশন ফাঁকা সেট হয় তবে এই দুইটা সেটকে বলা হয় Disjoint।
উদাহরণ - যদি A = {1, 3, 5} এবং B = {2, 4, 6} হয় তবে A ∩ B = ∅ হবে। এখানে A এবং B হলো Disjoint.
Difference of sets
দুইটা সেটের ডিফারেন্স বা পার্থক্য বলতে এমন একটা সেট বুঝায় যেখানে সেসব উপাদান থাকবে যা প্রথম সেটে আছে কিন্তু দ্বিতীয় সেটে নেই। ডিফারেন্সকে লেখা হয় A - B অথবা A\B এভাবে। A ও B এর ডিফারেন্সকে পড়া হয় complement
of B with respect to A বা A এর সাপেক্ষে B এর কমপ্লিমেন্ট।
কোনো উপাদান x, A - B এর সদস্য হবে যদি ও কেবল যদি x ∈ A এবং x ∉ B হয়। অর্থাৎ
A − B = {x ∣ x ∈ A ∧ x ∉ B}
হয়। নিচের এর ভেন ডায়াগ্রাম দেয়া হলো।
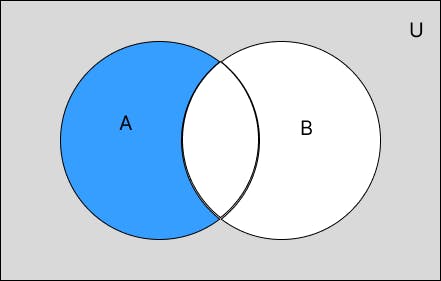
উদাহরণ - A = {1, 3, 5} and B = {1, 2, 3} হলে A - B = {5} হবে। কারণ 5 শুধু A তে আছে, B তে নেই।
Complement of sets
যদি U ইউনিভার্সাল সেট হয় তবে যেকোনো সেট A এর কমপ্লিমেন্টকে লেখা যায় U - A বা A'। অর্থাৎ U এর সাপেক্ষে A এর কমপ্লিমেন্টই হবে, A সেটের কমপ্লিমেন্ট।
কোনো উপাদান x, A' এর উপাদান হবে যদি ও কেবল যদি x ∉ A হয়, অর্থাৎ
A' = {x ∈ U ∣ x ∉ A}
হয়। নিচে ভেন ডায়াগ্রামের মাধ্যমে এটি দেখানো হলো -
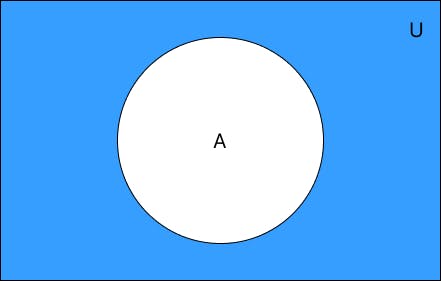
উদাহরণ - ০১ - যদি A = {a, e, i, o, u} হয়, যেখানে U হলো সমস্ত ইংরেজি বর্ণমালার সেট, তাহলে A' = {b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, y, z} হবে।
Set Identities
নিচে কিছু সেট আইডেন্টিটির একটা টেবিল দেয়া হলো যার মধ্যে কয়েকটা আমরা প্রমাণ করবো।
| Identity | Name |
| A ∩ U = A, A ∪ ∅= A | Identity laws |
| A ∪ U = U, A ∩ ∅= ∅ | Domination laws |
| A ∪ A = A, A ∩ A = A | Idempotent laws |
| (A')' = A | Complementation law |
| A ∪ B = B ∪ A, A ∩ B = B ∩ A | Commutative laws |
| A ∪ (B ∪ C) = (A ∪ B) ∪ C, A ∩ (B ∩ C) = (A ∩ B) ∩ C | Associative laws |
| A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) | Distributive laws |
| (A ∩ B)' = A' ∪ B', (A ∪ B)' = A' ∩ B' | De Morgan’s laws |
| A ∪ (A ∩ B) = A, A ∩ (A ∪ B) = A | Absorption laws |
| A ∪ A' = U, A ∩ A' = ∅ | Complement laws |
এগুলো প্রমাণ করার কয়েকটা উপায় আছে। আমরা একে একে সেগুলো দেখবো।
Subset method
যদি দুইটি সেট একে অপরের সাবসেট হয় তবে আমরা ধরে নিবো এই সেট দুইটি সমান।
প্রমাণ করুন (A ∩ B)’ = A’ ∪ B’
আমরা দুইটা সেট পরস্পরের সাবসেট এটা প্রমাণ করবো অর্থাৎ আমরা দেখাবো (A ∩ B)’ ⊆ A’ ∪ B’। যদি কোনো উপাদান x, (A ∩ B)’ এর মধ্যে থাকে তবে তা A’ ∪ B’ এর মধ্যেও থাকবে।
প্রথমে আমরা ধরি x ∈ (A ∩ B)’। কমপ্লিমেন্টের সংজ্ঞা অনুযায়ী আমরা বলতে পারি x ∉ A ∩ B। এরপর আমরা ইন্টারসেকশনের সংজ্ঞানুযায়ী দেখতে পারছি (x ∉ A) ∩ (x ∉ B) বা, (x ∉ A) ∧ (x ∉ B) বা, ¬((x ∈ A) ∧ (x ∈ B)) সত্য। প্রোপোজিশনের ডি মরগ্যান ল ব্যবহার করে আমরা পাই ¬(x ∈ A) or ¬(x ∈ B)। প্রোপোজিশনের নেগেশনের সংজ্ঞানুযায়ী আমরা পাই x ∉ A or x ∉ B। সেটের কমপ্লিমেন্ট এর সংজ্ঞানুযায়ী আমরা পাই x ∈ A’ or x ∈ B’। ইউনিয়নের সংজ্ঞানুযায়ী আমরা পাই x ∈ A’ ∪ B’। অর্থাৎ আমরা দেখাতে পারলাম (A ∩ B)’ ⊆ A’ ∪ B’।
এবার আমাদের দেখাতে হবে A’ ∪ B’ ⊆ (A ∩ B)’। অর্থাৎ যদি উপাদান x, A’ ∪ B’ এর মধ্যে আছে এটা যদি দেখাতে পারি তবে অবশ্যই (A ∩ B)’।
ধরি x ∈ A’ ∪ B’। ইউনিয়নের সংজ্ঞানুযায়ী আমরা পাই x ∈ A’ or x ∈ B’। এবার কমপ্লিমেন্টের সংজ্ঞানুযায়ী আমরা পাই x ∉ A or x ∉ B। তার মানে প্রোপোজিশন ¬(x ∈ A) ∨ ¬(x ∈ B) সত্য হবে। প্রোপোজিশনের ডি মরগ্যান ল থেকে আমরা পাই ¬((x ∈ A) ∧ (x ∈ B)) সত্য। তাহলে ইন্টারসেকশনের সংজ্ঞানুযায়ী আমরা পাচ্ছি ¬(x ∈ A ∩ B) বা, x ∈ (A ∩ B)’। তার মানে আমরা দেখাতে পারলাম A’ ∪ B’ ⊆ (A ∩ B)’।
যেহেতু আমরা দেখাতে পেরেছি দুইটি সেট পরস্পরের উপসেট সুতরাং এই দুইটি সেট সমান।
Set Builder Notation
সেট বিল্ডার নোটেশনের মাধ্যমে আমরা (A ∩ B)’ = A’ ∪ B’ এটা দেখাবো। এই প্রসেসের মাধ্যমে উপরের প্রসেসের মতো এত জটিল কথাবার্তা না লিখে আমরা কয়েকটা স্টেপে কাজটা সারবো।

দেখুন এটা অনেক সহজেই বোঝা যাচ্ছে।
Membership Table
উপরের দুইটা প্রসেস ছাড়াঅ আরো একভাবে দুইটা সেট যে সমান তা প্রমাণ করা যায়। সেটা হলো মেম্বারশীপ টেবিল। এটা অনেকটা প্রোপোজিশনের truth table এর মতোই।
চলুন আমরা মেম্বারশীপ টেবিলের মাধ্যমে A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) প্রমাণ করি।
| A | B | C | B ∪ C | A ∩ (B ∪ C) | A ∩ B | A ∩ C | (A ∩ B) ∪ (A ∩ C) |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
আমরা যদি একবার সেট আইডেন্টিটিগুলো প্রমাণ করতে পারি তাহলে আমরা সেগুলো নতুন আইডেন্টিটি প্রমাণের জন্য ব্যবহার করতে পারবো। যেমন আমরা এখন (A ∪ (B ∩ C) = (C’ ∪ B’) ∩ A’ প্রমাণ করবো।

Multisets
মাল্টিসেট হলো কিছু সদস্যের অবিন্যস্ত একটা সংগ্রহ যেখানে একটা সদস্য একাধিকবার সদস্য হিসেবে ব্যবহৃত হয়। আমরা সেটের মতোই সমস্ত নোটেশন ব্যবহার করবো, তবে প্রতিটা সদস্য কয়বার করে আছে তার নাম্বারটাও আমরা এখানে উল্লেখ করবো। অর্থাৎ আমাদের কাছে যদি এমন একটা সেট থাকে যেটা দেখতে এরকম {a, a, a, b, b, c, c, c, c}, যেখানে a আছে তিনটা, b আছে দুইটা এবং c আছে চারটা। এটা একটা মাল্টিসেট, এবং এটাকে আমাদের লিখতে হবে {3 . a, 2 . b, 4 . c} এভাবে। এখানে 3, 2, 4 এগুলোকে বলা হয় multiplicities।
আমরা এবার মাল্টিসেটের ইউনিয়ন, ইন্টারসেকশন, ডিফারেন্স এবং অ্যাডিশন দেখবো।
ধরি আমাদের দুইটা মাল্টিসেট আছে P = {4 . a, 1 . b, 3 . c} এবং Q = {3 . a, 4 . b, 2 . d}।
P ∪ Q = {max(4, 3) . a, max(1, 4) . b, max(3, 0) . c, max(0, 2) . d} = {4 . a, 4 . b, 3 . c, 2 . d}
অর্থাৎ দুইটা মাল্টিসেটের উপাদানের মধ্যে যেটার মাল্টিপ্লিসিটি বড় হবে সেটাই বসবে ইউনিয়নের ক্ষেত্রে।
P ∩ Q = {min(4, 3) . a, min(1, 4) . b, min(3, 0) . c, min(0, 2) . d} = {3 . a, 1 . b, 0 . c, 0 . d} = {3 . a, 1 . b}
অর্থাৎ দুইটা মাল্টিসেটের উপাদানের মধ্যে যেটার মাল্টিপ্লিসিটি ছোট হবে সেটাই বসবে ইন্টারসেকশনের ক্ষেত্রে।
P − Q = {(4 − 3) . a, (1 − 4) . b, (3 − 0) . c, (0 − 2) . d} = {1 . a, 0 . b, 3 . c, 0 . d} = {1 . a, 3 . c},
অর্থাৎ প্রথম মাল্টিসেটের উপাদানের মাল্টিপ্লিসিটি থেকে দ্বিতীয় সেটের উপাদানের মাল্টিপ্লিসিটি বাদ দিয়ে যা থাকবে সেটাই ডিফারেন্সের উপাদানগুলোর মাল্টিপ্লিসিটি হবে। কিন্তু যদি তা নেগেটিভ হয় তাহলে সেক্ষেত্রে মাল্টিপ্লিসিটি শূন্য বলে ধরে নেয়া হবে।
P + Q = {(4 + 3) . a, (1 + 4) . b, (3 + 0) . c, (0 + 2) . d} = {7 . a, 5 . b, 3 . c, 2 . d}
দুইটা মাল্টিসেটের উপাদানগুলোর মাল্টিপ্লিসিটির যোগফলই হবে নতুন সেটের উপাদানগুলোর মাল্টিপ্লিসিটি।
Conclusion
আশা করি সেট অপারেশন্স নিয়ে আপনারা ভালভাবেই বুঝতে পেরেছেন। পরের আর্টিকেলে আমরা ফাংশন নিয়ে আলোচনা করবো। ততক্ষণ পর্যন্ত এগুলো প্র্যাকটিস করতে থাকুন।

