Table of contents
- Introduction
- Topics we will learn in this article
- Valid Arguments in Propositional Logic
- Rules of Inference for Proportional Logic
- Using Rules of Inference to Build Arguments
- Resolution
- Fallacies
- Rules of Inference for Quantified Statements
- Combining Rules of Inference for Propositions and Quantified Statements
- Conclusion
Introduction
আমরা লজিক সম্পর্কে আগের আর্টিকেলগুলোতে অনেক কিছু জেনেছিলাম। মোটামুটি লজিক সম্পর্কে আমাদের আলোচনা শেষ। আমরা এই আর্টিকেল শেষে proofs সম্পর্কে জানবো। প্রুফস হলো কিছু ভ্যালিড আর্গুমেন্ট যারা গাণিতিক স্টেটমেন্টগুলোর সত্যতা প্রতিষ্ঠা করে থাকে। আর্গুমেন্ট বলতে আমরা সাধারণত কিছু স্টেটমেন্টের সিকোয়েন্স বুঝায় যা একটা conclusion এর মাধ্যমে সমাপ্ত হয়। একটা আর্গুমেন্ট ভ্যালিড হবে যদি ও কেবল যদি সকল premises true হয় এবং conclusion ও true হয়। ভ্যালিড আর্গুমেন্ট তৈরি করতে আমরা Rules of Inference নামে একটা কনসেপ্ট ব্যবহার করবো। এটা হলো আমাদের স্টেটমেন্ট এর সত্যতা যাচাই করার একটা বেসিক টুলস। এবং এটাই আমাদের এই আর্টিকেলের আলোচ্য বিষয়।
Topics we will learn in this article
- Valid Arguments in Propositional Logic
- Rules of Inference for Proportional Logic
- Using Rules of Inference to Build Arguments
- Resolution
- Fallacies
- Rules of Inference for Quantified Statements
- Combining Rules of Inference for Propositions and Quantified Statements
Valid Arguments in Propositional Logic
আমরা নিচের আর্গুমেন্টগুলো কনসিডার করি।
If you have a current password, then you can log onto the network.
You have a current password.
Therefore,
You can log onto the network.
আমরা এটা ভ্যালিড আর্গুমেন্ট কিনা তা বের করতে চাই। অর্থাৎ আমরা দেখতে চাই যে আমাদের conclusion বা You can log onto the network. অবশ্যই সত্য হবে যখন আমাদের premises বা If you have a current password, then you can log onto the network. এবং You have a current password. উভয়ই সত্য হবে।
আর্গুমেন্ট বলতে আমরা জেনেছিলাম কিছু স্টেটমেন্টের সিকোয়েন্স যা একটা conclusion দিয়ে শেষ হবে। এখানে তিনটা সিকোয়েন্সিয়াল স্টেটমেন্টস আছে যা একটা conclusion দিয়ে শেষ হয়েছে। সুতরাং এটা একটা আর্গুমেন্ট। এখন এটার ভ্যালিডিটি আলোচনা করার পূর্বে আমরা এটার form দেখবো। যদি p হয়, You have a current password. এবং q হয় You can log onto the network. তাহলে এই আর্গুমেন্টের ফর্ম দাঁড়াবে,
p → q
p
______
∴ q
এখানে ∴ এই চিহ্নটা সুতরাং বা therefore নির্দেশ করছে।
আমরা জানি যে p ও q প্রোপোজিশনাল ভ্যারিয়েবল হলে ((p → q) ∧ p) → q একটা Tautology, অর্থাৎ p → q এবং p উভয়ই সত্য হলে q অবশ্যই সত্য হবে। আমরা এটাকে একটা ভ্যালিড আর্গুমেন্ট বলতে পারি কারণ এখানে আমাদের সকল premises (শেষ স্টেটমেন্টের আগের স্টেটমেন্ট পর্যন্ত স্টেটমেন্টগুলোকে বলে premises) সত্য হলে আমাদের conclusion (শেষ স্টেটমেন্ট) অবশ্যই সত্য হবে। এখন ধরি If you have a current password, then you can log onto the network. এবং You have a current password. উভয়ই সত্য। তাহলে অবশ্যই আমাদের conclusion You can log onto the network. অবশ্যই সত্য হবে। তার মানে এই আর্গুমেন্ট একটা ভ্যালিড আর্গুমেন্ট।
এখন যদি p এবং p → q এর মধ্যে একটা সত্য না হয় তাহলে কি হবে? ধরি p হলো, You have access to the network এবং q হলো You can change your grade। ধরি p সত্য, কিন্তু p → q সত্য নয়। তাহলে এটাকে আমরা ভ্যালিড আর্গুমেন্ট হিসেবে বলতে পারবো না কারণ আমাদের একটা premise সত্য নয়, তাই আমরা বলতে পারছি না আমাদের conclusion সত্য হবে (বেশিরভাগ সময় এক্ষেত্রে conclusion false হয়)।
একটু ছোট করে উপরের সবকথা আরেকবার বুঝিয়ে দিই। আমাদেরকে একটা আর্গুমেন্ট দেয়া হলে আমরা প্রথমে সেটার প্রপোজিশনগুলোকে প্রপোজিশনাল ভ্যারিয়েবলে পরিবর্তিত করবো। ফলে আমাদের আর্গুমেন্ট একটা আর্গুমেন্ট ফর্মে পরিবর্তিত হবে। এরপর আমরা দেখবো আমাদের সমস্ত premises সত্য কিনা। যদি সত্য হয় তাহলে অবশ্যই conclusion ও সত্য হবে। সেক্ষেত্রে আমাদের আর্গুমেন্ট ভ্যালিড হবে। নাহয় ভ্যালিড হবে না।
কিছু প্রোপোজিশনের সিকোয়েন্সকে বলে আর্গুমেন্ট। ঐ আর্গুমেন্টের শেষের আগ পর্যন্ত প্রোপোজিশনগুলোকে বলে premises এবং শেষের প্রোপোজিশনকে বলে conclusion। একটা argument form হলো কিছু প্রোপোজিশনাল ভ্যারিয়েবলযুক্ত কম্পাউন্ড প্রোপোজিশনের সিকোয়েন্স। একটা আর্গুমেন্ট ভ্যালিড হবে যদি conclusion সত্য হয় যদি সকল premises সত্য হয়।
Rules of Inference for Proportional Logic
আমরা সবসময় একটা Truth Table ব্যবহার করে দেখাতে পারি যখন সকল premises true হবে, conclusion অবশ্যই সত্য হবে। কিন্তু এটা একটা বিশাল অপারেশন। চিন্তা করুন আমাদের ১০টা ভ্যারিয়েবল আছে। তাহলে truth table এর রুল অনুসারে রো সংখ্যা হবে 2^10 = 1024। সৌভাগ্যক্রমে আমাদের এই জটিল কাজে যেতে হবে না। কারণ আমাদের আছে rules of inference। এটি অনেক জটিল ভ্যালিড আর্গুমেন্ট তৈরিতে বিল্ডিং ব্লক হিসেবে কাজ করে।
বিগত টপিকে আমরা যে tautology দেখেছিলাম অর্থাৎ ((p → q) ∧ p) → q হলো rules of inference এর ভিত্তি যাকে modus ponens বা law of detachment বলা হয়। এই টটোলজি আমাদের একটা আর্গুমেন্ট ফর্ম দেয় যা আমরা আমাদের প্রথম আর্গুমেন্ট ভ্যালিডেশনে দেখেছিলাম। তা হলো -
p
p → q
______
∴ q
এই নোটেশন ব্যবহার করে আমরা প্রথমে আমাদের premises একটা কলামে লিখবো, এরপর একটা অনুভূমিক লাইন টানবো, এরপর ∴ দিবো এবং এর পাশে আমাদের conclusion লিখবো। অর্থাৎ modes ponens আমাদের বুঝাচ্ছে যে যদি আমাদের premises সত্য হয় তাহলে অবশ্যই conclusion সত্য হবে।
যেমন - যদি If it snows today, then we will go skiing এবং It is snowing today সত্য হয় তাহলে এদের conclusion We will go skiing, modes ponens অনুসারে অবশ্যই সত্য হবে।
আবার ধরি p হলো √2 > 3/2 এবং q হলো (√2)² > (3/2)²। এবার যদি modes ponens অনুসারে দেখি, p সত্য হলেও p → q সত্য নয় কারণ (√2)² > (3/2)² = 2 > 9/4 হতে পারে না। 2 < 9/4। সুতরাং যেহেতু একটা premise মিথ্যা হয়েছে সেক্ষেত্রে এই আর্গুমেন্ট ভ্যালিড নয়। আমরা rules of inference এর চার্টটা দেখি একটু।
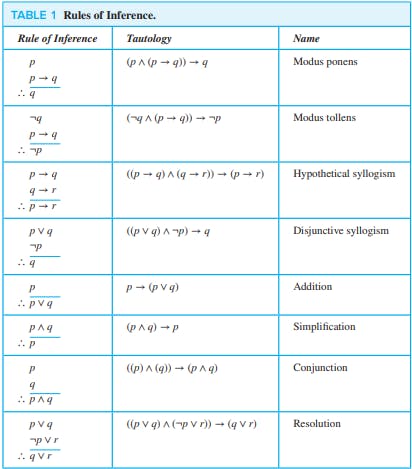
এবার একটা উদাহরণ দেখি।
উদাহরণ - ১ - আমাদের একটা আর্গুমেন্ট দেয়া আছে।
It is below freezing now. Therefore, it is below freezing or raining now.এটা ভ্যালিড কিনা আমাদের বের করতে হবে।
যদি p হয় It is below freezing now এবং q হয় It is raining now তাহলে আর্গুমেন্ট ফর্ম দাঁড়াবে -
p
______
∴ p ∨ q
আমরা চার্ট থেকে দেখতে পাচ্ছি যে এটা rules of inference এর addition রুল ফলো করে। সুতরাং এটি একটি ভ্যালিড আর্গুমেন্ট।
Using Rules of Inference to Build Arguments
এতক্ষণ পর্যন্ত আমরা দুইটি premises এর জন্য আর্গুমেন্ট দেখেছিলাম। এখন যদি অনেকগুলো premises থাকে এবং তাতে ভিন্ন ভিন্ন rules of inference এর ব্যবহার থাকে তাহলে সেই আর্গুমেন্ট ভ্যালিড কিনা তা কিভাবে করবো। নিচের দুইটা উদাহরণে তা স্টেপ বাই স্টেপ দেখানো হয়েছে। চলুন আমরা জেনে নিই -
উদাহরণ - ১ - আমাদের premises হলো
It is not sunny this afternoon and it is colder than yesterday,We will go swimming only if it is sunny,If we do not go swimming, then we will take a canoe tripএবংIf we take a canoe trip, then we will be home by sunset. আমাদের conclusion হলোWe will be home by sunset. আমাদের দেখাতে হবে premises lead to the conclusion.
প্রথমে আমরা আমাদের premises কে প্রোপোজিশনাল ভ্যারিয়েবলে প্রকাশ করি।
- p =
It is sunny this afternoon - q =
It is colder than yesterday - r =
We will go swimming - s =
We will take a canoe trip - t =
We will be home by sunset
তাহলে আমাদের premises দাঁড়াবে ¬p ∧ q, r → p, ¬r → s, s → t। আর conclusion দাঁড়াবে t. এবার আমাদের ভ্যালিড আর্গুমেন্ট দিতে হবে এগুলোর জন্য। আমরা একটা আর্গুমেন্ট ক্রিয়েট করবো। এবং এখানে আমরা পূর্বে উল্লেখিত চার্ট ব্যবহার করবো।
| Step | Reason |
| 1. ¬p ∧ q | Premise |
| 2. ¬p | Simplification using (1) |
| 3. r → p | Premise |
| 4. ¬r | Modus tollens using (2) and (3) |
| 5. ¬r → s | Premise |
| 6. s | Modus ponens using (4) and (5) |
| 7. s → t | Premise |
| 8. t | Modus ponens using (6) and (7) |
অর্থাৎ premises lead to conclusion. আমরা চাইলে truth table ব্যবহার করেও এটা দেখাতে পারতাম। কিন্তু সেক্ষেত্রে আমাদের ২^৫ = ৩২ টা রো নিতে হতো।
উদাহরণ - ২ - দেখান যে premises
If you send me an e-mail message, then I will finish writing the program,If you do not send me an e-mail message, then I will go to sleep earlyএবংIf I go to sleep early, then I will wake up feeling refreshedlead to the conclusionIf I do not finish writing the program, then I will wake up feeling refreshed.
যথারীতি আমরা প্রথমে প্রোপোজিশনাল ভ্যারিয়েবল নিয়ে নিই।
- p =
You send me an e-mail message - q =
I will finish writing the program - r =
I will go to sleep early - s =
I will wake up feeling refreshed
তাহলে আমাদের premises দাঁড়াবে p → q, ¬p → r, and r → s এবং conclusion হবে ¬q → s। এবার আমরা ভ্যালিড আর্গুমেন্ট নিবো।
| Step | Reason |
| 1. p → q | Premise |
| 2. ¬q → ¬p | Contrapositive of (1) |
| 3. ¬p → r | Premise |
| 4. ¬q → r | Hypothetical syllogism using (2) and (3) |
| 5. r → s | Premise |
| 6. ¬q → s | Hypothetical syllogism using (4) and (5) |
Resolution
কম্পিউটার প্রোগ্রামগুলো সাধারণত রিজনিং এর কাজগুলো অটোমেট করতে এবং এগুলোকে প্রমাণ করতে তৈরি করা হয়। এই প্রোগ্রামগুলোর মধ্যে অনেক প্রোগ্রাম rules of inference এর একটা resolution ব্যবহার করে। এটা যে টটোলজির উপর নির্ভর করে তা হলো - ((p ∨ q) ∧ (¬p ∨ r)) → (q ∨ r)। এই রেজ্যুলেশন রুলের ফাইনাল ডিসজাঙ্কশনকে বলা হয় resolvent। যখন আমরা q = r ধরবো তখন এটা দাঁড়াবে - (p ∨ q) ∧ (¬p ∨ q) → q. যখন আমরা r = F ধরবো তখন আমরা পাবো (p ∨ q) ∧ (¬p) → q এই টটোলজি যেটার উপর ভিত্তি করে তৈরি হয়েছে rules of inference এর অন্যতম একটা রুল rule of disjunctive syllogism।
রেজ্যুলেশন ব্যবহার করে দেখান যে
It is snowing or Bart is playing hockeyএবংJasmine is skiing or it is not snowingপ্রকাশ করেBart is playing hockey or Jasmine is skiing.
আমাদের প্রথম কাজ ভ্যারিয়েবল নেয়া। চলুন নিয়ে নিই -
- p =
It is snowing - q =
Bart is playing hockey - r =
Jasmine is skiing
রেজ্যুলেশন রুল ব্যবহার করে আমরা দেখতে পাচ্ছি p ∨ q এবং ¬p ∨ r প্রকাশ করে আমাদের conclusion q ∨ r।
Fallacies
অনেক কম fallacies ভুল আর্গুমেন্টে চলে আসে। এগুলো অনেকটা rules of inference এর অনুরূপ কিন্তু এগুলো টটোলজির জায়গায় কন্টিনজেন্সির উপর নির্ভর করে। এই টপিকে এগুলো সম্পর্কে আলোচনা করা হয়েছে ঠিক এবং ভুল রিজনিং এর মধ্যে পার্থক্য বুঝাতে।
প্রোপোজিশন ((p → q) ∧ q) → p একটা টটোলজি নয়। কারণ যখন p false এবং q true হবে তখন এটি false হবে। এছাড়াও অনেক ভুল আর্গুমেন্ট আছে যেগুলো টটোলজি হিসেবে ধরা হয়। অন্যভাবে বলতে গেলে এরা premises p → q ও q এবং conclusion p যুক্ত আর্গুমেন্টকে ভ্যালিড ফর্ম বলে ধরে নেয়। কিন্তু আসলে তা ভ্যালিড নয়। এই ধরণের ভুল যুক্তিকে বলা হয় fallacy of affirming the conclusion.
উদাহরণ - ১ঃ এই আর্গুমেন্ট কি ভ্যালিড?
If you do every problem in this book, then you will learn discrete mathematics.,You learned discrete mathematics.,Therefore, you did every problem in this book.
প্রথমে আমাদের ভ্যারিয়েবল ধরে নিই।
- p =
You did every problem in this book - q =
You learned discrete mathematics
তাহলে আমাদের premises দাঁড়ালো p → q এবং q। তার মানে আর্গুমেন্ট ফর্ম দাঁড়ালো if p → q and q, then p। কিন্তু এটা টটোলজি হতে পারে না। কারণ p false এবং q true হলে এটি false হবে। এটা একটা ভুল আর্গুমেন্টের উদাহরণ যা fallacy of affirming the conclusion ব্যবহার করে।
আরেকটা প্রপোজিশন আছে যেটা হলো ((p → q) ∧ ¬p) → ¬q, যেটাও টটোলজি নয়। কারণ এখানে p false এবং q true হলে এটা ফলস হবে। অনেক ভুল আর্গুমেন্ট ভুলবশত এটি rule of inference হিসেবে ব্যবহার করে। এই ধরণের ভুল রিজনিংকে বলা হয় fallacy of denying the hypothesis.
Rules of Inference for Quantified Statements
আমরা এতক্ষণ পর্যন্ত প্রোপোজিশনের জন্য Rules of Inference নিয়ে আলোচনা করেছি। এবার দেখবো কোয়ান্টিফায়ারযুক্ত স্টেটমেন্টের জন্য এটি কিভাবে কাজ করে।
Universal Instantiation - ধরেন আমাদের premise হলো
∀xP(x)। Universal Instantiation হলো rule of inference যেটা P(c) conclude করতে ব্যবহার করা হয় যেখানে c হলো একটা নির্দিষ্ট ডোমেইনের মেম্বার। অর্থাৎ Universal InstantiationAll women are wiseএই স্টেটমেন্ট থেকেLisa is wiseএই স্টেটমেন্ট conclude করে যেখানে Lisa সকল মহিলাম ডোমেইনের একজন মেম্বার।Universal Generalization - এটি আমরা তখন ব্যবহার করবো যখন আমরা দেখাবো যে আমাদের ডোমেইন থেকে ইচ্ছামতো একটা এলিমেন্ট c নিলে যদি P(c) সত্য হয় তখন ∀xP(x) সত্য হবে। মনে রাখতে হবে যে এলিমেন্ট c আমরা সিলেক্ট করবো সেটা যেন অবশ্যই একটা arbitrary (ইচ্ছামতো) এলিমেন্ট হয়, কোনো একটা নির্দিষ্ট এলিমেন্ট যেন না হয়। অর্থাত আমরা যখন ∀xP(x) থেকে c এর এক্সিস্টেন্স প্রমাণ করবো, তখন c এর উপর আমাদের কোনো কন্ট্রোল থাকবে না এবং আমরা অন্য কিছু assumption করতে পারবো না c এর জন্য।
Existential Instantiation - এই rule of inference আমাদের এটা প্রকাশ করতে সাহায্য করে যে ডোমেইনের একটা এলিমেন্ট c এর জন্য P(c) সত্য হবে যদি আমরা জানি যে ∃xP(x) সত্য। আমরা এখানে আমাদের ইচ্ছামতো c সিলেক্ট করতে পারবো না। সাধারণত আমাদের কোনো ধারণাই নেই c কি, শধু জানি এটা আছে। যেহেতু এটা আছে সেহেতু আমরা এর একটা নাম হিসেবে c দিতে পারি এবং আমাদের আর্গুমেন্ট কন্টিনিউ করতে পারি।
Existential generalization - এই rule of inference ব্যবহৃত হয় এটা বুঝতে যে, ∃xP(x) সত্য হবে যখন ডোমেইনের একটা নির্দিষ্ট এলিমেন্ট c আমাদের জানা থাকবে যার জন্য P(c) সত্য হবে। অর্থাৎ যদি আমরা জানি যে এরকম একটা এলিমেন্ট c ডোমেইনের মধ্যে আছে যার জন্য P(c) সত্য হবে তাহলে আমরা বুঝবো যে ∃xP(x) সত্য হবে।
উপরের রুলগুলোকে সামারাইজ করে নিচের টেবিল আকারে দেখাবো হলো -
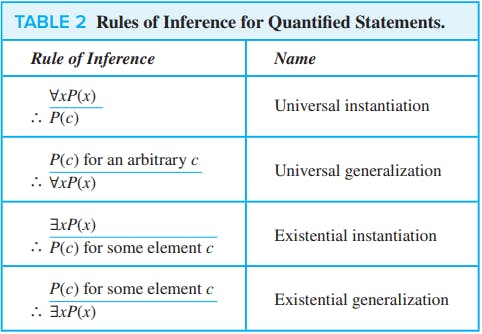
দেখান যে
Everyone in this discrete mathematics class has taken a course in computer scienceএবংMarla is a student in this classএই premisesMarla has taken a course in computer scienceএই conclusion প্রকাশ করে।
প্রথমে আমরা আমাদের প্রোপোজিশনাল ফাংশন ধরে নিই -
- D(x) - x is in this discrete mathematics class
- C(x) = “x has taken a course in computer science
তাহলে আমাদের premises দাঁড়ালো ∀x(D(x) → C(x)) এবং D(Marla) এবং conclusion হলো C(Marla)।
এবার আগের মতো আমাদের স্টেপগুলো বের করতে হবে -
| Step | Reason |
| 1. ∀x(D(x) → C(x)) | Premise |
| 2. D(Marla) → C(Marla) | Universal instantiation from (1) |
| 3. D(Marla) | Premise |
| 4. C(Marla) | Modus ponens from (2) and (3) |
দেখান যে
A student in this class has not read the bookএবংEveryone in this class passed the first examএই premisesSomeone who passed the first exam has not read the book.এই conclusion প্রকাশ করে।
- C(x) - x is in this class
- B(x) - x has read the book
- P(x) - x passed the first exam.
premises হবে ∃x(C(x) ∧ ¬B(x)) এবং ∀x(C(x) → P(x)), conclusion হবে ∃x(P(x) ∧ ¬B(x))। এবার স্টেপগুলো দেখি আমরা।
| Step | Reason |
| 1. ∃x(C(x) ∧ ¬B(x)) | Premise |
| 2. C(a) ∧ ¬B(a) | Existential instantiation from (1) |
| 3. C(a) | Simplification from (2) |
| 4. ∀x(C(x) → P(x)) | Premise |
| 5. C(a) → P(a) | Universal instantiation from (4) |
| 6. P(a) | Modus ponens from (3) and (5) |
| 7. ¬B(a) | Simplification from (2) |
| 8. P(a) ∧ ¬B(a) | Conjunction from (6) and (7) |
| 9. ∃x(P(x) ∧ ¬B(x)) | Existential generalization from (8) |
Combining Rules of Inference for Propositions and Quantified Statements
এতক্ষণ পর্যন্ত আমরা প্রোপোজিশন এবং কোয়ান্টিফায়ার উভয়ের ক্ষেত্রেই rule of inference এর কাজ দেখেছি। উপরের টপিকের উদাহরণে আমরা universal instantiation এবং modus ponens ব্যবহার করেছিলাম। আমরা প্রায়ই এই কম্বিনেশন ব্যবহার করবো। এই কম্বিনেশনকে বলা হয় universal modus ponens। এই রুল আমাদেরকে বুঝায় যে যদি ∀x(P(x) → Q(x)) সত্য হয় এবং ইউনিভার্সাল কোয়ান্টিফায়ারের ডোমেইনের একটা নির্দিষ্ট এলিমেন্ট a এর জন্য যদি P(a) সত্য হয়, তবে Q(a) অবশ্যই সত্য হবে।
∀x(P(x) → Q(x))
P(a), where a is a particular element in the domain
______
∴ Q(a)
আরেকটা গুরুত্বপূর্ণ রুল আছে যেটাকে বলে universal modus tollens. এটা universal instantiation এবং modus tollens এর কম্বিনেশন।
∀x(P(x) → Q(x))
¬Q(a), where a is a particular element in the domain
______
∴ ¬P(a)
Conclusion
এই চাপটার পুরোপুরি লজিকও ছিল না আবার পুরোপুরি প্রুফও ছিল না। প্রুফের জন্য এটা একটা গুরুত্বপূর্ণ ক্লাস ছিল। কারণ এই টপিক বুঝতে না পারলে আমরা প্রুফ ভালভাবে বুঝতে পারবো না। পরবর্তী ক্লাস থেকে প্রুফ শুরু হবে। এবং প্রুফ নিয়ে বিস্তারিত আলোচনা করা হবে।

