Introduction

গত আর্টিকেলে আমরা Universal quantifiers এবং Existential quantifiers নিয়ে আলোচনা করেছিলাম এবং দেখেছিলাম কিভাবে এগুলোর মাধ্যমে গাণিতিক স্টেটমেন্টসমূহ রিপ্রেজেন্ট করা যায়। এছাড়াও আমরা দেখেছিলাম কিভাবে ইংরেজি বা যেকোনো ভাষাকে লজিক্যাল এক্সপ্রেশনে রূপান্তরিত করা যায়।

আজ আমরা Quantifiers এর উপর আরেকটা টপিক সম্পর্কে জানবো যার নাম Nested Quantifiers। এর মানে হলো একটা কোয়ান্টিফায়ার আরেকটা কোয়ান্টিফায়ারের স্কোপের মধ্যে থাকবে। স্কোপ সম্পর্কে আমরা গত আর্টিকেলে বলেছিলাম। আপনারা সেখান থেকে একটু দেখে নিবেন। যেমন -

∀x∃y(x + y = 0)

একটা জিনিস বলে রাখা ভাল, স্কোপের মধ্যে যা কিছু থাকবে তাকে প্রোপোজিশনাল ফাংশন হিসেবে গণ্য করা যায়। যেমন উপরের কোয়ান্টিফায়ারকে আমরা ∀xQ(x) হিসেবে কল্পনা করতে পারি, যেখানে Q(x) হলো ∃yP(x, y), যেখানে P(x, y) হলো x + y = 0।

নেস্টেড কোয়ান্টিফায়ার কম্পিউটার সায়েন্স এবং গণিতে বিশদভাবে ব্যবহৃত হয়। কখনও কখনও আমাদের এই নেস্টেড কোয়ান্টিফায়ার বুঝতে সমস্যা হয়ে যায়। আমরা আগের আর্টিকেলে আমাদের প্রাপ্ত জ্ঞান দিয়ে সেগুলো বুঝতে পারি। এই আর্টিকেলে আমরা নেস্টেড কোয়ান্টিফায়ার সম্পর্কে ভালভাবে জানবো। আমরা দেখবো কিভাবে The sum of two positive integers is always positive. এই ধরণের গাণিতিক বিবৃতিকে নেস্টেড কোয়ান্টিফায়ারের মাধ্যমে প্রকাশ করা যায় এবং কিভাবে Everyone has exactly one best friend এই ধরণের বাক্যকে লজিক্যাল স্টেটমেন্টে নেস্টেড কোয়ান্টিফায়ারের মাধ্যমে ট্রান্সলেট করা যায়।

Topics we will cover in this article

• Understanding Statements Involving Nested Quantifiers
  • Thinking of Quantification as Loops
• The Order of Quantifiers
• Translating Mathematical Statements into Statements Involving Nested Quantifiers
• Translating from Nested Quantifiers into English
• Translating English Sentences into Logical Expressions
• Negating Nested Quantifiers

Understanding Statements Involving Nested Quantifiers

এই টপিকটা বুঝার জন্য আগে আমরা কিছু উদাহরণ দেখি।

• উদাহরণ - ১ঃ ধরি x এবং y দুইটা ভ্যারিয়েবল এবং এদের ডোমেইন হলো সকল বাস্তব সংখ্যা। আমাদের স্টেটমেন্ট হলো ∀x∀y(x + y = y + x)। এটা বুঝাচ্ছে সব বাস্তব সংখ্যা x এবং y এর জন্য x + y এবং y + x সমান হবে।
• উদাহরণ - ২ঃ এবার আমাদের স্টেটমেন্ট হলো ∀x∃y(x + y = 0) এবং ডোমেইন আগের মতো সকল বাস্তব সংখ্যা। এটা বুঝাচ্ছে প্রতিটা বাস্তব সংখ্যা x এর জন্য এমন একটা y এর মান পাবো যার জন্য x + y = 0 হবে।
• উদাহরণ - ৩ঃ আমাদের স্টেটমেন্ট হলো ∀x∀y∀z(x + (y + z) = (x + y) + z) এবং ডোমেইন যথারীতি সকল বাস্তব সংখ্যা। এটাও বুঝাচ্ছে সকল বাস্তব সংখ্যা x, y এবং z এর জন্য x + (y + z) = (x + y) + z হবে।
• উদাহরণ - ৪ঃ ∀x∀y((x > 0) ∧ (y < 0) → (xy < 0)) এই স্টেটমেন্টকে ইংরেজিতে ট্রান্সলেট করতে হবে যেখানে ডোমেইন হলো সকল বাস্তব সংখ্যা। এটা বুঝাচ্ছে সকল বাস্তব সংখ্যা x এবং y এর জন্য যদি x > 0 এবং y < 0 হয় তবে xy < 0 হবে। অর্থাৎ যদি x positive এবং y negative হয় তাহলে x এবং y এর গুণফল নেগেটিভ হবে। এটাকে যদি আমরা ইংরেজিতে লিখি তাহলে হবে The product of a positive real number and a negative real number is always a negative real number.

Thinking of Quantification as Loops

উপরের চারটা উদাহরণ দেখে কি আপনারা নেস্টেড কোয়ান্টিফায়ারের কনসেপ্ট বুঝতে পারছেন? কিছু কিছু হয়তো বুঝতে পেরেছেন। এবার আপনি নেস্টেড কোয়ান্টিফায়ারকে নেস্টেড ফর লুপ বা যেকোনো লুপের সাথে তুলনা করেন। কিছু কি মাথায় আসছে? আচ্ছা আমি একটু হেল্প করি আপনাদের।

• ধরেন আমাদের কাছে একটা স্টেটমেন্ট আছে যেটা হলো ∀x∀yP(x, y)। এখন এটা সত্য কিনা তা প্রমাণ করার জন্য আমরা প্রথমে x এর জন্য একটা লুপ চালাবো। এবার প্রতিটা x এর ভ্যালুর জন্য y এর উপর লুপ চালাবো। যদি x এর প্রতিটা ভ্যালুর জন্য y এর যে ভ্যালু পাবো সেটার জন্য P(x, y) সত্য হয়ে তবে ∀x∀yP(x, y) সত্য হবে। আর যদি যেকোনো একটা y এর ভ্যালুর জন্যও P(x, y) মিথ্যা হয় তাহলে এই স্টেটমেন্ট মিথ্যা হবে। এই কথাগুলোকে আমরা যদি একটা ফর লুপের মাধ্যমে দেখি তাহলে আরো মাথায় ঢুকবে -

for(x = initial value; some condition for x or domain; changes value for x) {
  for(y = x; some condition for y or domain; changes value for y) {
    // check the proposition for P(x,y)
  }
  if (P(x, y) is true for all values of y for all values of x) {
    ∀x∀yP(x, y) = true
  } else {
    ∀x∀yP(x, y) = false
  }
}

ফর লুপের কিছুই হয়নি যদিও। এটা শুধু আপনাদেরকে বুঝানোর জন্য একটু চেষ্টা করলাম। আশা করি ব্যাপারটা ধরতে পেরেছেন আপনারা।

• এবার আমরা দেখবো ∀x∃yP(x, y) সত্য কিনা তা। তার জন্য আমাদের প্রথমে x এর জন্য লুপ চালাতে হবে। এরপর প্রতিটা x এর ভ্যালুর জন্য আমরা y এর উপর লুপ চালাবো যতক্ষণ না পর্যন্ত অন্তত y এর একটা ভ্যালুর জন্য P(x,y) সত্য না হচ্ছে। যদি y এর একটা ভ্যালুর জন্যও P(x, y) সত্য হয়ে তবে স্টেটমেন্ট সত্য হবে। আর যদি এমন কোনো y এর ভ্যালু পাওয়া না যায় যার জন্য P(x, y) সত্য হবে তাহলে সেক্ষেত্রে স্টেটমেন্ট মিথ্যা হবে।

for(x = initial value; some condition for x or domain; changes value for x) {
  for(y = x; some condition for y or domain; changes value for y) {
    // check the proposition for P(x,y)
  }
  if (P(x, y) is true for at least one value of y for all values of x) {
    ∀x∃yP(x, y) = true
  } else {
    ∀x∃yP(x, y) = false
  }
}

• ∃x∀yP(x, y) এর ক্ষেত্রে আমরা x এর উপর লুপ চালাবো যতক্ষণ না পর্যন্ত অন্তত একটা x এর ভ্যালু না পাচ্ছি যার জন্য যখন y এর উপর লুপ চালাবো তখন y এর সকল ভ্যালুর জন্য P(x, y) সত্য না হচ্ছে। যখন আমরা x এর এরকম একটা ভ্যালু পাবো তখন ∃x∀yP(x, y) সত্য হবে। নাহয় মিথ্যা হবে।

for(x = initial value; some condition for x or domain; changes value for x) {
  for(y = x; some condition for y or domain; changes value for y) {
    // check the proposition for P(x,y)
  }
  if (P(x, y) is true for all values of y for at least one value of x) {
    ∃x∀yP(x, y) = true
  } else {
    ∃x∀yP(x, y) = false
  }
}

• ∃x∃yP(x, y) এর ক্ষেত্রে আমরা x এর উপর লুপ চালাবো। এরপর x এর প্রতিটা ভ্যালুর জন্য y এর উপর লুপ চালাবো যতক্ষণ না পর্যন্ত অন্তত একটা x এর ভ্যালুর জন্য অন্তত একটা y ভ্যালু না পাচ্ছি যার জন্য P(x, y) সত্য হবে। যদি এরকম কোনো x এবং y এর ভ্যালু পাই তাহলে ∃x∃yP(x, y) সত্য হবে। নাহয় মিথ্যা হবে।

for(x = initial value; some condition for x or domain; changes value for x) {
  for(y = x; some condition for y or domain; changes value for y) {
    // check the proposition for P(x,y)
  }
  if (P(x, y) is true for at least one value of y for at least one value of x) {
    ∃x∃yP(x, y) = true
  } else {
    ∃x∃yP(x, y) = false
  }
}

আশা করি নেস্টেড কোয়ান্টিফায়ারের কনসেপ্ট এখন পরিষ্কার হয়ে গেছে আপনাদের। একটু প্র্যাকটিস করলে পুরোপুরি বুঝে যাবেন।

The Order of Quantifiers

অনেক গাণিতিক স্টেটমেন্টে একাধিক ভ্যারিয়েবলযুক্ত প্রপোজিশনাল ফাংশনের একাধিক কোয়ান্টিফায়ার থাকতে পারে। সেক্ষেত্রে order of quantifiers বুঝাটা খুবই গুরুত্বপূর্ণ যদি না সবগুলো universal quantifier হয় বা সবগুলো existential quantifier হয়। এটা বুঝার জন্য আমরা নিচের উদাহরণগুলোর দিকে একটু তাকাতে হবে।

উদাহরণ - ১ঃ যদি P(x, y) বলতে x + y = y + x বুঝায় তাহলে ∀x∀yP(x, y) এবং ∀y∀xP(x, y) এর truth values কি হবে যদি ডোমেইন সকল বাস্তব নাম্বার হয়?

∀x∀yP(x, y) এই স্টেটমেন্ট বুঝাচ্ছে For all real numbers x, for all real numbers y, x + y = y + x., অর্থাৎ সকল বাস্তব সংখ্যা x এবং সকল বাস্তব সংখ্যা y এর জন্য x + y = y + x হবে। তার মানে এটা সত্য।

এখন ∀y∀xP(x, y) এর জন্যও একই জিনিসই বুঝাচ্ছে অর্থাৎ সকল বাস্তব সংখ্যা y এবং সকল বাস্তব সংখ্যা x এর জন্য x + y = y + x হবে. তার মানে এটাও সত্য হবে।

আমরা যেমনটা বলেছিলাম যদি সব একই কোয়ান্টিফায়ার হয় সেক্ষেত্রে order of quantifiers গুরুত্বপূর্ণ হয় না। এক্ষেত্রে সকল কোয়ান্টিফায়ার ইউনিভার্সাল তাই যে অর্ডারেই তা করা হোক না কেন, সকল ক্ষেত্রেই truth value একই আসবে।

উদাহরণ -২ঃ যদি Q(x, y) বলতে x + y = 0 বুঝায় তাহলে ∃y∀xQ(x, y) এবং ∀x∃yQ(x, y) এর truth values কি হবে যদি ডোমেইন সকল বাস্তব নাম্বার হয়?

∃y∀xQ(x, y) এই স্টেটমেন্টের জন্য প্রপোজিশন হচ্ছে There is a real number y such that for every real number x, Q(x, y). অর্থাৎ যেকোনো একটা বাস্তব সংখ্যা y এর জন্য যে সকল x এর ভ্যালু পাওয়া যাবে তার জন্য Q(x, y) সত্য হবে। কিন্তু বাস্তবে এমন কোনো বাস্তব সংখ্যা y পাওয়া যায় না যার সকল x ভ্যালুর জন্য x + y = 0 হবে। যেমন যদি y এর ভ্যালু ২ হয় তাহলে শুধুমাত্র x এর ভ্যালু -২ হলেই ২ - ২ = ০ হবে। x এর প্রতিটা ভ্যালুর জন্য আন্সার শূন্য হবে না। তাই এই স্টেটমেন্টটা মিথ্যা।

আবার ∀x∃yQ(x, y) এর প্রপোজিশন বুঝাচ্ছে For every real number x there is a real number y such that Q(x, y). অর্থাৎ প্রতিটা x এর ভ্যালুর জন্য একটা y এর ভ্যালু আছে যার জন্য x + y = 0 হবে। যে ব্যাখ্যাটা উপরে দিয়েছিলাম। তার মানে এই ক্ষেত্রে স্টেটমেন্ট সত্য হবে। কারণ x এর মান ২ হলে y এর মান শুধু -২ হতে পারবে, x = 3 হলে y = -3 হতে পারবে শুধু। অর্থাৎ x এর মান যাই হোক না কেন y = -x হতে পারবে শুধু। অন্য কোনো ভ্যালু না। তাই এই স্টেটমেন্টটা সত্য হবে।

এক্ষেত্রে কোয়ান্টিফায়ার ভিন্ন ভিন্ন। তাই যদি ভিন্ন অর্ডারে করা হয় ভিন্ন ভিন্ন truth value আসবে। যেটা আপনারা উপরের ব্যাখ্যা থেকেই বুঝতে পারছেন। একই ডোমেইন, একই প্রপোজিশনাল ফাংশন। শুধু order of quantifiers ভিন্ন হওয়ার কারণে truth value চেইঞ্জ হয়ে গেলো। এই বিষয়টা আপনারা মাথায় রাখবেন ভালভাবে।

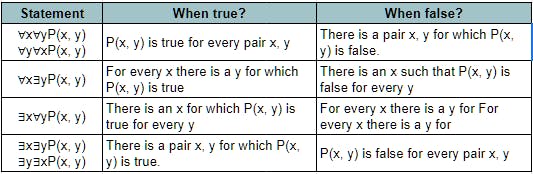
Translating Mathematical Statements into Statements Involving Nested Quantifiers

ম্যাথমেটিকাল স্টেটমেন্টকে আমরা কিভাবে নেস্টেড কোয়ান্টিফায়ারযুক্ত লজিক্যাল এক্সপ্রেশনে কনভার্ট করতে পারি তা এই টপিকের আলোচ্য বিষয়। চলুন দেখি।

• The sum of two positive integers is always positive এই বাক্যকে লজিক্যাল এক্সপ্রেশনে রূপান্তরিত করতে হবে।

এটার জন্য প্রথমে আমাদের এই বাক্যটাকে অন্যভাবে একটু সাজিয়ে লিখতে হবে। ধরি ঐ দুইটা পজিটিভ ইন্টিজার x এবং y. তাহলে আমরা লিখতে পারি For all positive integers x and y, x + y is positive.। এটাকে যদি আমরা এক্সপ্রেশনে প্রকাশ করি তাহলে দাঁড়াবে ∀x∀y((x > 0) ∧ (y > 0) → (x + y > 0)) যেখানে দুই ভ্যারিয়েবলের ডোমেইন হলো সকল ইন্টিজার। এখন আমরা যদি বলি দুইটা ভ্যারিয়েবলের ডোমেইনই হলো পজিটিভ ইন্টিজার সেক্ষেত্রে (x > 0) ∧ (y > 0) কন্ডিশনটা আর দিতে হবে না। কারণ আমরা ডোমেইনে বলেই দিয়েছি এগুলো পজিটিভ ইন্টিজারই হবে। সুতরাং সেটাকে আরো সিমপ্লিফাই করে লেখা যায় ∀x∀y(x + y > 0), যেখানে x এবং y উভয়ের ডোমেইন পজিটিভ ইন্টিজার।

• Every real number except zero has a multiplicative inverse. এই বাক্যকে লজিক্যাল এক্সপ্রেশনে রূপান্তর করুন।

মাল্টিপ্লিকেটিভ ইনভার্স মানে হলো যদি দুইটা রিয়েল নাম্বার x এবং y হয় তবে এদের মাল্টিপ্লিকেটিভ ইনভার্স হবে xy = 1। এবার যদি বাক্যটাকে আমাদের মতো করে ভ্যারিয়েবল ব্যবহার করে সাজাই তাহলে পাবো, For every real number x, if x ≠ 0, then there exists a real number y such that xy = 1. অর্থাৎ ∀x((x ≠ 0) → ∃y(xy = 1))।

Translating from Nested Quantifiers into English

নেস্টেড কোয়ান্টিফায়ারযুক্ত এক্সপ্রেশনকে ইংরেজিতে রূপান্তর করা একটু জটিল। আমাদের প্রথমে বের করতে হবে এর predicates and quantifiers কি বুঝাচ্ছে। এরপর এদেরকে একটা সিম্পল বাক্যে এক্সপ্রেস করতে হবে। চলুন দেখি কিভাবে করা যায়।

• ∀x(C(x) ∨ ∃y(C(y) ∧ F(x, y))) কে ইংরেজি বাক্যে লিখুন যেখানে C(x) হলো 'x has a computer' এবং F(x, y) হলো 'x and y are friends' যেখানে x এবং y উভয়েরই ডোমেইন হলো ক্লাসের সকল ছাত্রছাত্রী।

এটার মানে বুঝাচ্ছে ক্লাসে প্রতিটা ছাত্র x এর একটা কম্পিউটার আছে অথবা ক্লাসে এমন একজন ছাত্র আছে y যার কম্পিউটার আছে এবং x ও y দুইজন বন্ধু। এটাকে যদি ইংরেজিতে রূপান্তর করি তাহলে হবে For every student x of the class, x has a computer or there is a student y in the class such that y has a computer and x and y are both friends.। আরো সহজভাবে যদি লিখি তাহলে হবে Every student in the clas has a computer or has a friend who has a computer.

• ∃x∀y∀z((F(x, y) ∧ F(x, z) ∧ (y ≠ z)) → ¬F(y, z)) কে ইংরেজি বাক্যে লিখুন যেখানে F(a, b) মানে হলো a এবং b দুইজন বন্ধু এবং x, y, z এর ডোমেইন হলো ক্লাসের সকল ছাত্রছাত্রী।

প্রথমে আমরা (F(x, y) ∧ F(x, z) ∧ (y ≠ z)) → ¬F(y, z) কে সিমপ্লিফাই করি। এর মানে দাঁড়াচ্ছে যদি x ও y বন্ধু হয়, এবং x & z বন্ধু হয় এবং y ও z একই মানুষ না হয় তাহলে y ও z বন্ধু না। যদি এবার স্টেটমেন্টকে আমরা বাক্যে সাজাই তাহলে হবে there is a student x such that for all students y and all students z other than y, if x and y are friends and x and z are friends, then y and z are not friends। আরো সিমপ্লিফাই করলে দাঁড়াবে, there is a student none of whose friends are also friends with each other. অর্থাৎ এমন একজন ছাত্র যার বন্ধুরা পরস্পরের বন্ধু নয়।

Translating English Sentences into Logical Expressions

• If a person is female and is a parent, then this person is someone’s mother বাক্যটাকে লজিক্যাল এক্সপ্রেশনে প্রকাশ করুন যেখানে ডোমেইন হলো সকল মানুষ।

আমরা প্রথমে এটাকে একটু আমাদের মতো করে সাজিয়ে লিখলে পাবো এমন একজন মানুষ x আছেন, যদি তিনি একজন মহিলা হন এবং একজন অভিভাবক হন তাহলে এমন একজন মানুষ y আছে যার মা হচ্ছেন x। যদি F(x) 'x is female' হয়, P(x) 'x is a parent' হয় এবং M(x, y) 'x is the mother of y' হয় তাহলে লজিক্যাল এক্সপ্রেশন দাঁড়াবে ∀x((F(x) ∧ P(x)) → ∃yM(x, y)) বা ∀x∃y((F(x) ∧ P(x)) → M(x, y))।

• There is a woman who has taken a flight on every airline in the world এই বাক্যকে কোয়ান্টিফায়ার ব্যবহার করে লজিক্যাল এক্সপ্রেশনে রূপান্তরিত করতে হবে। যেখানে ডোমেইন হলো পৃথিবীর সকল মহিলা, সকল ফ্লাইট এবং সকল এয়ারলাইন।

ধরি P(w, f) হলো 'w has taken f', Q(f, a) হলো 'f is a flight of a'। তাহলে আমরা আমাদের এক্সপ্রেশন লিখতে পারি ∃w∀a∃f(P(w, f ) ∧ Q(f, a))। আশা করি বুঝতে পেরেছেন। একটু বুঝলে কিন্তু খুবই সহজ। এবার এটাকে যদি আমরা প্রপোজিশনাল ফাংশনের মাধ্যমে প্রকাশ করি তাহলে দাঁড়াবে ∃w∀a∃fR(w, f, a) যেখানে R(w, f, a) হলো 'w has taken f on a'।

Negating Nested Quantifiers

• ∀x∃y(xy = 1) কে নেগেশনে এক্সপ্রেস করতে হবে।

আমরা আর্টিকেল 1.4 এ দেখেছিলাম De Morgan's laws for quantifiers। সেটা থেকে আমরা জানি আমাদের স্টেটমেন্টের নেগেশন অর্থাৎ ¬∀x∃y(xy = 1) হলো ∃x¬∃y(xy = 1) এর ইক্যুইভ্যালেন্ট, যেটা আবার ∃x∀y¬(xy = 1) এর ইক্যুইভ্যালেন্ট। আবার ¬(xy = 1) কে লেখা যায় xy ≠ 1। তাহলে আমাদের এক্সপ্রেশন দাঁড়ালো ∃x∀y(xy ≠ 1)।

• There is a woman who has taken a flight on every airline in the world এর নেগেশন করতে হবে।

এর নেগেশন হবে There does not exist a woman who has taken a flight on every airline in the world। প্রথমে আমাদেরকে লজিক্যাল এক্সপ্রেশন বের করে নিতে হবে। এটা অলরেডি আমরা করেছি উপরে। তবে যেহেতু এখানে লিখেছে কোনো মহিলা ফ্লাইট ধরেনি তাই আমাদের এক্সপ্রেশন হবে ¬∃w∀a∃f(P(w, f ) ∧ Q(f, a))। এবার এটাকে আমরা ইক্যুইভ্যালেন্সের সিকোয়েন্স অনুসারে সাজাই।

¬∃w∀a∃f(P(w, f ) ∧ Q(f, a)) ≡ ∀w¬∀a∃f(P(w, f ) ∧ Q( f, a)) 
≡ ∀w∃a¬∃f(P(w, f ) ∧ Q( f, a)) 
≡ ∀w∃a∀f¬(P(w, f ) ∧ Q( f, a)) 
≡ ∀w∃a∀f(¬P(w, f ) ∨ ¬Q( f, a))

সর্বশেষ স্টেটমেন্ট অর্থাৎ ∀w∃a∀f (¬P(w, f ) ∨ ¬Q( f, a)) প্রকাশ করছে For every woman there is an airline such that for all flights, this woman has not taken that flight or that flight is not on this airline যা আমাদের প্রশ্নে দেয়া বাক্যের নেগেশন প্রকাশ করছে।

Conclusion

আজকের আর্টিকেলের পর আশা করি আপনারা যেকোনো বাক্যের লজিক্যাল এক্সপ্রেশন, নেস্টেড কোয়ান্টিফায়ার বের করতে পারবেন। সেই সাথে যেকোনো নেস্টেড কোয়ান্টিফায়ারকে বাক্যে রূপান্তর, এর নেগেশন বের করা এসবও আশা করি খুব সহজেই করতে পারবেন। পরবর্তী ক্লাসে আমরা আলোচনা করবো Rules of Inference নিয়ে যেটা আরেকটা গুরুত্বপূর্ণ টপিক।