Introduction

ধরেন আপনার কাছে একটা কম্পাউন্ড প্রোপোজিশন আছে যার একটা truth value আছে (true or false)। এখন আপনি আরেকটি কম্পাউন্ড প্রোপোজিশন পেলেন যার truth value ও একই। আমরা চাইলে প্রথম প্রোপোজিশনকে সেকেন্ড প্রপোজিশন দিয়ে রিপ্লেস করতে পারি। একে বলা হয় প্রোপোজিশনাল ইক্যুইভ্যালেন্স। এটি খুবই গুরুত্বপুর্ণ একটি টপিক। কারণ এর মাধ্যমে যে মেথডগুলো পাওয়া যায় তা অন্য আর্গুমেন্ট তৈরি করতে সাহায্য করে। আর্গুমেন্ট সম্পর্কে আমরা পরবর্তীতে আরো বিস্তারিত জানবো। আমরা এই আর্টিকেলে প্রোপোজিশনাল ইকুইভ্যালেন্স নিয়ে বিস্তারিত আলোচনা করবো।

Topics we will cover in this article

আমরা এই আর্টিকেলে যে যে টপিক নিয়ে আলোচনা করবো তা হলো -

• Tautology, Contradiction and Contingency
• Logical Equivalences
  • Logical Equivalence
  • A simple technique to create truth tables
• Using De Morgan's Laws
• Constructing New Logical Equivalences

চলুন তাহলে শুরু করা যাক।

Tautology, Contradiction and Contingency

প্রোপোজিশনাল ইক্যুইভ্যালেন্স নিয়ে আলোচনা শুরুর আগে আমাদের কিছু টার্মস সম্পর্কে জানতে হবে। সেগুলো হলো - Tautology, Contradiction and Contingency। চলুন এগুলো কি জিনিস একটু দেখে নেয়া যাক।

• Tautology - একটা কম্পাউন্ড প্রোপজিশনের প্রোপোজিশনাল ভ্যারিয়েবলের Truth ভ্যালু যাই থাক না কেন, প্রোপোজিশন যদি সবসময় true হয় তাহলে তাকে Tautology বলা হয়। আমরা একটা উদাহরণ দেখি Tautology এর। আমরা প্রমাণ করবো যে p ∨ ¬p একটা Tautology। 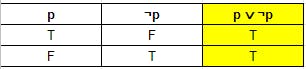দেখুন এখানে p এর Truth ভ্যালু যাই হোক না কেন p ∨ ¬p সবসময় true। সুতরাং এটা একটা Tautology।

• Contradiction - এটা হচ্ছে Tautology এর উলটো। তার মানে এটা সবসময় ফলস হবে ভ্যারিয়েবলের Truth ভ্যালু যাই থাক না কেন। আমরা দেখার চেষ্টা করি p ∧ ¬p একটা Contradiction কিনা। 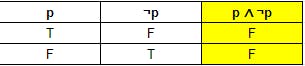দেখুন এখানে p ∧ ¬p এর মান সবসময় ফলস। তাই এটা একটা Contradiction।

• Contingency - একটা কম্পাউন্ড প্রোপোজিশন যেটা Tautology ও না বা Contradiction ও না তাকে বলে Contingency। তার মানে এখানে true এবং false দুই রকমেরই রেজাল্ট আসবে। এটার উদাহরণ আমরা আগেও অনেক দেখেছি এবং ভবিষ্যতেও দেখবো। তাই আলাদাভাবে আর দেখালাম না এখানে।

গাণিতিক যুক্তির ক্ষেত্রে Tautology এবং Contradiction খুবই গুরুত্বপূর্ণ বিষয়।

Logical Equivalences

যে সকল কম্পাউন্ড প্রোপোজিশনের সকল সম্ভাব্য কেইসের জন্য একই Truth ভ্যালু পাওয়া যাবে তাদেরকে বলা হয় Logically Equivalent. ধরুন, p ↔ q যদি Tautology হয় তাহলে p এবং q লজিক্যালি ইক্যুইভ্যালেন্ট হবে এবং একে লেখা যায় p ≡ q। অনেক ক্ষেত্রে ≡ এর পরিবর্তে ⇔ চিহ্নটাও ব্যবহার করা হয়। এই চিহ্নটা কিন্তু লজিক্যাল কোনো অপারেটর নয় এবং p ≡ q কোনো কম্পাউন্ড প্রোপোজিশন না। এটা জাস্ট p ↔ q যে একটা Tautology সেটা প্রকাশ করে।

De Morgan's Laws লজিক্যাল ইক্যুইভ্যালেন্সের ভাল উদাহরণ। যেমন -

• ¬(p ∧ q) ≡ ¬p ∨ ¬q
• ¬(p ∨ q) ≡ ¬p ∧ ¬q

যখন কোনো ∧ বা ∨ অপারেটরের সাথে ¬ অপারেটর যুক্ত হবে তখন ঐ অপারেটরগুলো চেইঞ্জ হয়ে যাবে। অর্থাৎ কনজাঙ্কশন অপারেটর ডিসজাঙ্কশন হয়ে যাবে এবং ডিসজাঙ্কশন অপারেটর কনজাঙ্কশন হয়ে যাবে।

এবার আমরা লজিক্যাল ইক্যুইভ্যালেন্স নিয়ে কিছু প্র্যাকটিস করি।

উদাহরণ - ১ - দেখান যে ¬(p ∨ q) ≡ ¬p ∧ ¬q।

এটা দেখার জন্য আমরা ¬(p ∨ q) এবং ¬p ∧ ¬q Truth ভ্যালু কম্পেয়ার করবো। যদি এদের Truth ভ্যালু একই হয় তাহলে ¬(p ∨ q) এবং ¬p ∧ ¬q লজিক্যালি ইক্যুইভ্যালেন্ট হবে। দেখুন এখানে ¬(p ∨ q) এবং ¬p ∧ ¬q এর Truth ভ্যালুগুলো একদম সেইম টু সেইম। তার মানে এই দুইটা লজিক্যালি ইক্যুইভ্যালেন্ট।

উদাহরণ - ২ - এবার আমরা দেখবো p → q ≡ ¬p ∨ q লজিক্যালি ইক্যুইভ্যালেন্ট কিনা।

প্রথমে যথারীতি আমাদের Truth ভ্যালু বের করতে হবে। 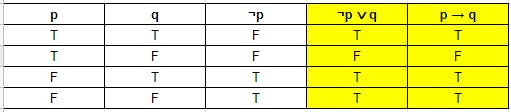যেহেতু p → q এবং ¬p ∨ q এর Truth ভ্যালু একই তার মানে p → q ≡ ¬p ∨ q। এটাকে বলা হয় conditional-disjunction equivalence.

উদাহরণ - ৩ - এবার আমরা দেখবো p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) কিনা।

এখানে এসে আপনারা একটু আটকে যেতে পারেন। এতদিন ধরে আমরা দুইটা ভ্যারিয়েবলের জন্য Truth টেবিল বানিয়েছিলাম। সেখানে রো ছিল ৪টা। যেখানে Truth ভ্যালুগুলো সহজেই বসিয়ে দিতে পেরেছি। কিন্তু এই উদাহরণে ভ্যারিয়েবল ৩টা এবং রো হবে ২ to the power ৩ অর্থাৎ ৮ টা। এবং কলাম ৩টা। এখানে Truth ভ্যালু বসাতে গেলে অর্ধেক যাওয়ার পরে আমরা গুলিয়ে ফেলি। আমি আপনাদের একটা টেকনিক শিখিয়ে দিচ্ছি যেটা ব্যবহার করে আপনারা সহজেই Truth টেবিল তৈরি করে ফেলতে পারবেন।

A simple technique to create truth tables

• আমাদের ভ্যারিয়েবলগুলো হলো p, q and r। অর্থাৎ ৩টা। আমাদের রো হবে ৮টা এবং কলাম ৩টা। প্রথমে আপনারা প্রথম ভ্যারিয়েবল অর্থাৎ p এর কলামে প্রথম অর্ধেক রো অর্থাৎ চারটা রো আপনারা T দিয়ে পূরণ করবেন এবং পরবর্তী অর্ধেক অর্থাৎ পরবর্তী চারটা রো F দিয়ে পূরণ করবেন।

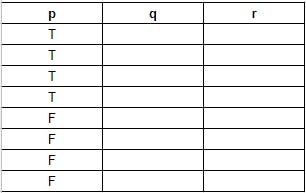
• এরপর আসি দ্বিতীয় ভ্যারিয়েবলের কলামে অর্থাৎ q এর কলামে। এখানে আপনি আগের কলামে প্রথম যতটা রো T বসিয়েছেন তার অর্ধেক রো T দিয়ে পূরণ করবেন এবং পরবর্তী ততো রো F দিয়ে পূরণ করবেন। এভাবে শেষ না হওয়া পর্যন্ত চলতে থাকবে। অর্থাৎ এক্ষেত্রে যেহেতু আমরা আগের কলাম মানে p এর ক্ষেত্রে প্রথম চার ঘর T দিয়ে পূরণ করেছিলাম তাই এখানে প্রথম দুই ঘর T, পরের দুই ঘর F এভাবে করে চলতে থাকবো শেষ না হওয়া পর্যন্ত।

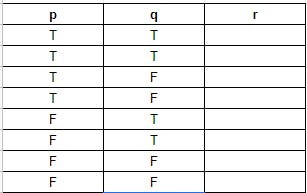
• r এর ক্ষেত্রে ক্ষেত্রেও ঠিক আগের কলামের প্রথম কয় ঘর T দিয়ে পূরণ হয়েছে দেখতে হবে। তার অর্ধেক ঘর অর্থাৎ এক্ষেত্রে যেহেতু q এর প্রথম দুই ঘর T দিয়ে পূরণ হয়েছে তার অর্ধেক অর্থাৎ একটা ঘর T, একটা ঘর F এভাবে করে চলতে থাকবো যতক্ষণ রো শেষ না হয়।

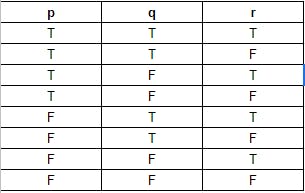
এভাবে যদি ৪টা ভ্যারিয়েবল থাকে তাহলে রো হবে ১৬টা। p এর ক্ষেত্রে প্রথম ৮টা T এবং পরের ৮টা F দিয়ে পূরণ করবেন। q এর ক্ষেত্রে p এর প্রথম যতটা T আছে তার অর্ধেক বা ৮ এর অর্ধেক অর্থাৎ ৪টা T, ৪টা F এভাবে। r এর ক্ষেত্রে q এর প্রথম যতটা T আছে তার অর্ধেক বা ৪ এর অর্ধেক অর্থাৎ ২টা T, ২টা F এভাবে এবং ফাইনালি s এর ক্ষেত্রে r এর প্রথম যতটা T আছে তার অর্ধেক বা ২ এর অর্ধেক অর্থাৎ ১টা T, ১টা F এভাবে পূরণ করবেন। আমি একটা ডেমো শেয়ার করলাম আপনাদের সাথে।

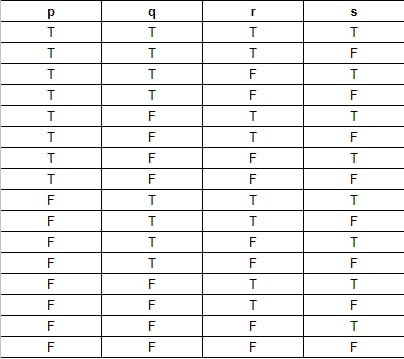
এবার আমরা আমাদের উদাহরণে ফিরে যায়। আমাদের দেখানোর কথা ছিল p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) কিনা।

প্রথমে Truth টেবিলটা রেডি করি। 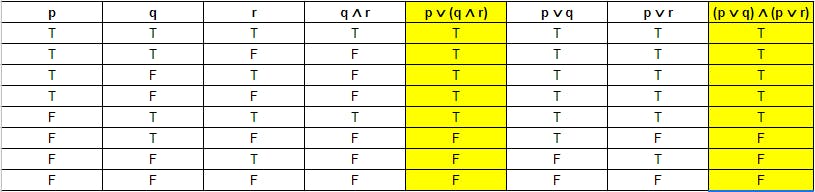অর্থাৎ দেখা যাচ্ছে p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)। একে বলা হয় distributive law of disjunction over conjunction.

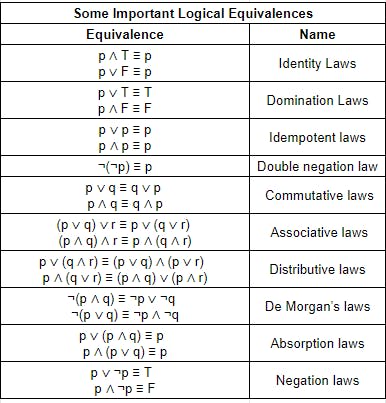
এবার আমরা কিছু লজিক্যাল ইক্যুইভ্যালেন্সের চার্ট দেখবো। আপনাদের কাজ হলো Truth টেবিল ব্যবহার করে এগুলো যে আসলেই ইক্যুইভ্যালেন্ট সেগুলো প্রমাণ করা।

List of some logical equivalences

• Some Important Logical Equivalences

• Logical Equivalences involving Conditional Statements

  • p → q ≡ ¬p ∨ q
  • p → q ≡ ¬q → ¬p
  • p ∨ q ≡ ¬p → q
  • p ∧ q ≡ ¬(p → ¬q)
  • ¬(p → q) ≡ p ∧ ¬q
  • (p → q) ∧ (p → r) ≡ p → (q ∧ r)
  • (p → r) ∧ (q → r) ≡ (p ∨ q) → r
  • (p → q) ∨ (p → r) ≡ p → (q ∨ r)
  • (p → r) ∨ (q → r) ≡ (p ∧ q) → r

• Logical Equivalences involving Conditional Statements

  • p ↔ q ≡ (p → q) ∧ (q → p)
  • p ↔ q ≡ ¬p ↔ ¬q
  • p ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q)
  • ¬(p ↔ q) ≡ p ↔ ¬q

এবার আপনাদের কাজ হলো এই সবগুলো ইক্যুইভ্যালেন্স Truth টেবিল ব্যবহার করে প্রমাণ করা নিজে নিজে। যদি Truth টেবিল বুঝে থাকেন তাহলে এই কাজটা পারা কোনো ব্যাপারই না আপনাদের জন্য। আমার বিশ্বাস আপনারা পারবেন।

Using De Morgan's Laws

ডি মরগ্যান ল অনেক গুরুত্বপূর্ণ। এরা আমাদের কিভাবে কনকাঙ্কশনকে এবং ডিসজাঙ্কশনকে নেগেট করতে হয় সেটার ধারণা দেয়। আরো নির্দিষ্টভাবে যদি বলি ¬(p ∧ q) ≡ ¬p ∨ ¬q এই ইক্যুইভ্যালেন্স থেকে আমরা দেখতে পারছি একটা কনজাঙ্কশনের নেগেশন, ভ্যারিয়েবলগুলোর আলাদা আলাদাভাবে নেগেশনের ডিসকাঙ্কশনের ইক্যুইভ্যালেন্ট। আবার ¬(p ∨ q) ≡ ¬p ∧ ¬q এই ইক্যুইভ্যালেন্স থেকে আমরা পাচ্ছি একটা ডিসজাঙ্কশনের নেগেশ্‌ ভ্যারিয়েবলগুলোর আলাদা আলাদাভাবে নেগেশনের কনজাঙ্কশনের ইক্যুইভ্যালেন্ট। আমরা এই সূত্রগুলোর একটা বাস্তব উদাহরণ দেখি।

উদাহরণ - ১ - Use De Morgan’s laws to express the negations of “Miguel has a cellphone and he has a laptop computer” and “Heather will go to the concert or Steve will go to the concert.”

প্রথম ক্ষেত্রে আমরা p হিসেবে ধরি "Miguel has a cellphone" এবং q হিসেবে ধরি "Miguel has a laptop computer". এবার যদি আমরা লজিকে রূপান্তর করি তাহলে এই স্টেটমেন্টটা দাঁড়াবে p ∧ q. ডি মরগ্যান ল এর ইক্যুইভ্যালেন্স থেকে আমরা জানি ¬(p ∧ q) ≡ ¬p ∨ ¬q। সুতরাং আমরা এই স্টেটমেন্টের নেগেশনকে লিখতে পারি এভাবে - Miguel does not have a cellphone or he does not have a laptop computer.

দ্বিতীয় ক্ষেত্রে আমরা p হিসেবে ধরি "Heather will go to the concert" এবং q হিসেবে ধরি "Steve will go to the concert". এবার যদি আমরা লজিকে রূপান্তর করি তাহলে এই স্টেটমেন্টটা দাঁড়াবে p ∨ q. ডি মরগ্যান ল এর ইক্যুইভ্যালেন্স থেকে আমরা জানি ¬(p ∨ q) ≡ ¬p ∧ ¬q। সুতরাং আমরা এই স্টেটমেন্টের নেগেশনকে লিখতে পারি এভাবে - Heather will not go to the concert and Steve will not go to the concert.

Constructing New Logical Equivalences

আমরা পূর্বে যে লজিক্যাল ইক্যুইভ্যালেন্সের লিস্ট দেখেছিলাম সেগুলো ব্যবহার করে অন্য আরো লজিক্যাল ইক্যুইভ্যালেন্স তৈরি করতে পারে। একটা কম্পাউন্ড প্রোপোজিশনের Truth ভ্যালু চেইঞ্জ করা ছাড়া সেই কম্পাউন্ড প্রোপোজিশনের কোনো একটা প্রোপোজিশন আরেকটা কম্পাউন্ড প্রোপোজিশন দ্বারা রিপ্লেস করা যায়। পরবর্তী উদাহরণগুলোতে আমরা তেমন কিছু টেকনিক শিখবো। আপনারা বলতে পারেন আমরা তো অলরেডি পারি। Truth টেবিল ব্যবহার করে। হ্যাঁ আমরা পারি। তবে এবার Truth টেবিল ব্যবহার করবো না। এবার আমরা আমাদের লিস্টের মেথডগুলো ব্যবহার করবো। কিভাবে? চলুন দেখি।

• উদাহরণ - ১ - Show that ¬(p → q) ≡ p ∧ ¬q.

• উদাহরণ - ২ - Show that ¬(p ∨ (¬p ∧ q)) ≡ ¬p ∧ ¬q.

• উদাহরণ - ৩ - Show that (p ∧ q) → (p ∨ q) is a tautology.

Conclusion

প্রোপোজিশনাল ইক্যুইভ্যালেন্সেস খুবই গুরুত্বপূর্ন একটি টপিক। আমি এখানে একটা ধারণা দেয়ার চেষ্টা করলাম। আপনাকে যদি একদম মাথার মধ্যে গেঁথে ফেলতে হয় তবে প্র্যাকটিসের কোনো বিকল্প নেই। এটা দেখতে মনে হয় খুবই সহজ। কিন্তু যখন আপনি নিজে চেষ্টা করতে যাবেন দেখবেন অনেক চিন্তাভাবনার বিষয় আছে এতে। তাই আমি বলবো, আপনারা খুব ভালভাবে এই টপিকটা প্র্যাকটিস করবেন যতক্ষণ না পর্যন্ত কনফিডেন্স পাচ্ছেন। পরের আর্টিকেলে আমরা Predicates and Quantifiers নিয়ে আলোচনা করবো। ততক্ষণ পর্যন্ত আপনারা এটা ভালভাবে প্র্যাকটিস করুন।