Introduction
গণিত, কম্পিউটার সায়েন্স এবং অন্যান্য ডিসিপ্লিনে লজিকের অনেক ধরণের প্রয়োগ রয়েছে। সাধারণত গণিত, বিজ্ঞান এবং আমরা যে ভাষায় কথা বলি সেগুলোর মাধ্যমে স্টেটমেন্ট বা বিবৃতিগুলো আমাদের কাছে অতটা স্পষ্ট হয় না। সেগুলোকে স্পষ্ট করে তোলার জন্য লজিক্যাল ভাষায় ট্রান্সলেট করা হয়। যেমন সফটওয়্যার এবং হার্ডওয়্যার ডেভেলপমেন্টের পূর্বেই এদের স্পেসিফিকেশনগুলো পুঙ্খানুপূঙ্খভাবে সাজিয়ে নিতে হয়। এই কাজটি করার জন্য লজিক ব্যবহার করা হয়ে থাকে। এছাড়াও কম্পিউটার সার্কিট ডিজাইনের জন্য, কম্পিউটার প্রোগ্রাম তৈরি করতে, প্রোগ্রাম ঠিক নাকি ভুল পরীক্ষা করতে এবং এক্সপার্ট সিস্টেম বিল্ড করতে প্রোপোজিশনাল লজিক ব্যবহার করা হয়ে থাকে। বিভিন্ন পাজল সলভ করার জন্যও প্রোপোজিশনাল লজিক ব্যবহার করা হয়ে থাকে। আমরা এই আর্টিকেলে সেরকম কিছু অ্যাপ্লিকেশন নিয়ে আলোচনা করবো।
Topics we will cover in this article
- Translating English Sentences
- System Specifications
- Boolean Searches
- Logic Puzzles
- Logic Circuits
Translating English Sentences
কেন আমাদের শুধু শুধু ইংরেজি বা যে কোনো ভাষার স্টেটমেন্টকে লজিক্যাল ভাষায় ট্রান্সলেট করতে হবে? এর অনেকগুলো কারণ আছে। প্রথম কারণ হচ্ছে, ইংরেজি বা যেকোনো ভাষার স্টেটমেন্ট সাধারণত আমরা যা চাই সেভাবে আমাদেরকে স্পষ্টভাবে স্টেটমেন্ট দিতে পারে না। ভাষার মাধ্যমে আমরা লজিক্যাল যে ব্যাপারস্যাপার সেগুলো খুব সহজে বা স্পষ্টভাবে বুঝতে পারি না। আমরা যদি সেটা লজিক্যাল ভাষায় ট্রান্সলেট করে ফেলি তাহলে সেটা আমাদের কাছে সহজবোধ্য এবং ক্লিয়ার হয়ে যাবে। এছাড়াও যদি আমরা একবার ভাষা থেকে লজিক্যাল এক্সপ্রেশনে ট্রান্সলেট করে ফেলি, তাহলে এই এক্সপ্রেশনগুলো অ্যানালাইসিস করে আমরা এদের truth ভ্যালু বের করে ফেলতে পারবো, এদেরকে প্রয়োজনবোধে ম্যানিপুলেট করতে পারবো এবং rules of interference (চাপটার 1.6 এ এটা নিয়ে আলোচনা করা হবে) ব্যবহার করতে পারবো।
জানি এসব কথাবার্তা মাথার উপর দিয়ে যাচ্ছে। উদাহরণ না দিলে কিছুতেই তা মাথায় ঢুকবে না। আসুন আমরা উদাহরণ দেখি।
- উদাহরণ - ১ঃ
You can access the internet from campus only if you are a computer science major or you are not a freshman.কিভাবে এই স্টেটমেন্টকে আমরা লজিক্যাল এক্সপ্রেশনে রূপান্তর করতে পারি? চলুন দেখি।
প্রথমে আমরা আমাদের প্রোপোজিশনগুলোকে আলাদা করে ফেলি। আমরা স্টেটমেন্ট দেখেই বুঝতে পারছি এখানে ৩টা প্রোপোজিশন আছে। সেগুলো আমরা p (You can access the internet from campus), q (you are a computer science major), r (you are a freshman) হিসেবে ধরে নিলাম। এবার আমরা গত আর্টিকেলে যা শিখেছিলাম সেগুলোর আলোকে নিচের এক্সপ্রেশনটা লিখতে পারি।
p → (q ∨ ¬r)
একটু কনফিউশন লাগতে পারে কারো কারো হয়তো, যে আমরা তো জানি if এর সাথে যা থাকে তাই p হয়। কিন্তু এখানে আছে only if. 'p only if q' যে কথা, 'if p, then q' ও একই কথা। আরো অনেকভাবে কন্ডিশনাল স্টেটমেন্ট লেখা যায়।আমরা দেখলাম কিভাবে একটা ইংরেজি বাক্যকে লজিক্যাল এক্সপ্রেশনে রূপান্তর করা যায়। এই এক্সপ্রেশনটার দিকে তাকালেই আমরা এর মিনিংটা বুঝতে পারছি। ভাষায় একটা বাক্যকে অনেক ভাবে লেখা যায়। তার উদাহরণ আপনারা এখনই পেলেন। if p, then q এবং p only if q একই মনোভাব প্রকাশ করছে। এই দুইটা ছাড়াও আরো আছে। তার মানে একটা মিনিং অনেকভাবে প্রকাশ করা যায়। যেটা মাঝে মাঝে কনফিউশনের সৃষ্টি করতে পারে। কিন্তু লজিক্যাল এক্সপ্রেশনে একভাবেই তা প্রকাশ করা যায়। তাই আমরা এক্সপ্রেশনের দিকে তাকালেই সহজে বুঝে যায় এটা কি বলতে চাইছে। এবং এর truth ভ্যালু বের করতে পারি।
আরেকটা উদাহরণ দেখি।
- উদাহরণ - ২ঃ
You cannot ride the roller coaster if you are under 4 feet tall unless you are older than 16 years old.
ধরি p, q, r যথাক্রমে you are under 4 feet tall, you are older than 16 years old এবং you can ride the roller coaster. এখানে বুঝাচ্ছে যদি তুমি ১৬ বছরের উপর না হও এবং তোমার হাইট ৪ ফুটের নিচে হয় তাহলে তুমি রোলার কোস্টারে চড়তে পারবে না। এবার আমাদের লজিক্যাল এক্সপ্রেশনটা লিখে ফেলি।
(p ∧ ¬q) → ¬r
এই এক্সপ্রেশন থেকে সহজেই বোঝা যাচ্ছে আমাদের স্টেটমেন্ট কি বুঝাতে চাইছে।
System Specifications
যেকোনো ভাষাকে লজিক্যাল এক্সপ্রেশনে রূপান্তরের কনসেপ্টটা হার্ডওয়্যার এবং সফটওয়্যার উভয় সিস্টেমের জন্যই গুরুত্বপূর্ণ। সিস্টেম ইঞ্জিনিয়ার এবং সফটওয়্যার ইঞ্জিনিয়াররা নরমাল ভাষার একটা রিকোয়ারমেন্ট পায়। সেটাকে তারা নিখুঁতভাবে লজিক্যাল এক্সপ্রেশনের মাধ্যমে স্পেসিফিকেশনে কনভার্ট করে, যেটা সিস্টেম ডেভেলপমেন্টের ভিত্তি হিসেবে কাজ করে। আমরা একটা উদাহরণ দেখলে সেটা ক্লিয়ার হয়ে যাবে।
- উদাহরণ - ১ঃ Express the specification “The automated reply cannot be sent when the file system is full” using logical connectives.
আমরা প্রথমে p এবং q দুইটা ভ্যারিয়েবল নিলাম এবন এদের প্রোপোজিশন হলো যথাক্রমে The automated reply can be sent এবং the file system is full। উপরের স্টেটমেন্টকে আমরা এভাবে বলতে পারি If the file system is full, then the automated reply cannot be sent. সেটাকে যদি আমরা লজিক্যাল এক্সপ্রেশনে প্রকাশ করি তাহলে দাঁড়াবে এরকম q → ¬p.
সিস্টেম স্পেসিফিকেশন সবসময় কনসিস্টেন্ট হতে হবে। অর্থাৎ এতে এমন কোনো conflicting স্পেসিফিকেশন থাকতে পারবে না যেটা পরবর্তীতে contradiction বা অসংগতির সৃষ্টি করে। যদি একটা সিস্টেম কনসিস্টেন্ট না হয় তাহলে সব স্পেসিফিকেশন স্যাটিসফাই করে এমন কোনো সিস্টেম ডেভেলপ করার কোনো উপায় নেই। আমরা নিচের উদাহরণটি দেখলে বুঝবো।
- উদাহরণ- ২ঃ Determine whether these system specifications are consistent:
- “The diagnostic message is stored in the buffer or it is retransmitted.”
- “The diagnostic message is not stored in the buffer.”
- “If the diagnostic message is stored in the buffer, then it is retransmitted.”
এগুলো কনসিস্টেন্ট কিনা তা বের করার আগে আমাদের বের করতে হবে এদের লজিক্যাল এক্সপ্রেশন। আমরা p = The diagnostic message is stored in the buffer এবং q = The diagnostic message is retransmitted যদি ধরি তাহলে এদের এক্সপ্রেশনগুলো দাঁড়াবে এরকম -
- p ∨ q
- ¬p
- p → q
যদি আমাদের এই ৩টা স্টেটমেন্ট true হতে হয় তাহলে অবশ্যই ১ এবং ৩ এ p কে ফলস হতে হবে শুধু ২ নাম্বারকে true করার জন্য। যদি p ফলস হয় এবং q true হয় তাহলে ডিসজাঙ্কশন এবং কন্ডিশনালের নিয়মে 1 and 3 অবশ্যই ট্রু হবে। তার মানে দেখা যাচ্ছে যদি ২ নাম্বারে p ফলসও হয় তাহলেও আমরা তিনটা স্টেটমেন্টই true পাচ্ছি। সুতরাং আমরা এই সিদ্ধান্তে আসতে পারি যে এটা একটা কনসিস্টেন্ট সিস্টেম। অর্থাৎ একটা সিস্টেম তখনই কনসিস্টেন্ট হবে যখন এদের প্রতিটা স্পেসিফিকেশন স্যাটিসফাই করবে।
যদি এখানে এমন কোনো স্টেটমেন্ট থাকতো যেটার কারণে আমাদের রিকোয়ারমেন্ট কোনোভাবেই মিট করা যাচ্ছিলো না তাহলে সেক্ষেত্রে এই সিস্টেম কনসিস্টেন্ট হতো না।
Boolean Searches
লজিক্যাল কানেক্টিভসমূহ কোনো ইনফরমেশনের একটা বিশাল কালেকশন খুঁজে বের করতে ব্যাপকভাবে ব্যবহৃত হয়। উদাহরণস্বরূপ ওয়েব পেইজের ইন্ডেক্সের কথা বলা যায়। কারণ এই সার্চিংসমূহ প্রোপোজিশনাল লজিকের কৌশল ব্যবহার করে। এদেরকে সাধারণত Boolean Searches বলা হয়ে থাকে। বুলিয়ান সার্চে connective AND ব্যবহৃত হয় দুইটা সার্চ আইটেমই আছে এমন রেকর্ড ম্যাচ করার কাজে। Connective OR ব্যবহার হয় দুইটা বা দুইটার যেকোনো একটা সার্চ আইটেম ম্যাচ করার কাজে এবং connective NOT ব্যবহার হয় যেকোনো একটা নির্দিষ্ট সার্চ আইটেম বাদ দেয়ার জন্য। আমরা এটা বুঝার জন্য একটা উদাহরণ দেখি। বুলিয়ান সার্চ ব্যবহার করে কিভাবে ওয়েব পেইজ সার্চ করা হয় একটু বুঝার চেষ্টা করি।
এখন অনেক সার্চ ইঞ্জিন বুলিয়ান সার্চ টেকনিক সাপোর্ট করে। এটি একটা নির্দিষ্ট সাবজেক্টের সমস্ত ওয়েব পেইজ খোঁজার ক্ষেত্রে খুবই উপকারী। ধরেন আমরা সার্চ করলাম 'universities in New Mexico'। এখন নিউ মেক্সিকোর সমস্ত ইউনিভার্সিটির ওয়েব পেইজ পেতে আমাদের খুঁজতে হবে এমন সব পেইজ যারা NEW AND MEXICO AND UNIVERSITIES এটা ম্যাচ করে। এটা আমাদেরকে NEW, MEXICO, UNIVERSITIES এই তিনটা শব্দ আছে এমন ওয়েব পেইজগুলো শো করবে। এর ফলে অন্য অনেক পেইজও সার্চে চলে আসতে পারে। যেমন new Universities in Mexico এর রেজাল্টও আসতে পারে কারণ এখানে NEW, MEXICO, UNIVERSITIES এই তিনটা শব্দই আছে। এখন অনেক সার্চ ইঞ্জিন অবশ্য কোনো নির্দিষ্ট phrase খুঁজার জন্য কোটেশন মার্ক ব্যবহার করে। এটা ব্যবহার করে আমরা 'NEW MEXICO' এবং 'UNIVERSITIES' ম্যাচ করে এমন পেইজ খুঁজে বের করতে পারি।
এরপর আমরা 'universities in New Mexico or Arizona' সার্চ করলাম। সেক্ষেত্রে আমাদের ম্যাচ করাতে হবে (NEW AND MEXICO OR ARIZONA) AND UNIVERSITIES. আমরা গত আর্টিকেলে দেখেছিলাম precedence অনুসারে AND এর কাজ আগে হবে। সুতরাং প্রথম ক্ষেত্রে (NEW MEXICO OR ARIZONA) এভাবে কাজ করবে। তার মানে এটা আমাদের এমন পেইজসমূহ দেখাবে যেখানে UNIVERSITIES এবং NEW MEXICO অথবা ARIZONA শব্দগুলো আছে।
এবার আমরা চাইছি 'universities in Mexico' (not New Mexico)। আমাদের প্রথমে দেখতে হবে কোন কোন পেইজগুলো MEXICO AND UNIVERSITIES এই টার্মটা ম্যাচ করছে। কিন্তু এখানে একটা সমস্যা আছে। সেটা হলো যেহেতু New Mexico তেও Mexico আছে সেহেতু সেখানের ইউনিভার্সিটির লিস্টও আমাদের কাছে চলে আসবে। কিন্তু আমরা তা চাই না। তাই এক্ষেত্রে ভাল হয় যদি (MEXICO AND UNIVERSITIES) NOT NEW এটা যেসব পেইজ ম্যাচ করবে তাদের রেজাল্ট দেখানো। তাহলে কোন পেইজে যদি NEW থাকে বুলিয়ান সার্চের মাধ্যমে তা বাদ পড়ে যাবে। আমরাও অযথা কিছু অপ্রয়োজনীয় পেইজ দেখবো না।
Logic Puzzle
লজিক্যাল রিজনিং এর মাধ্যমে যে পাজলগুলো সলভ করা হয় তাদেরকে বলে লজিক্যাল পাজল। লজিকের নিয়মগুলো প্র্যাকটিস করার জন্য এই লজিক্যাল পাজলগুলো অত্যন্ত উপকারী। এছাড়াও লজিক্যাল রিজনিং এর জন্য যে কম্পিউটার প্রোগ্রাম ডিজাইন করা হয় সেখানে প্রায়ই লজিক্যাল পাজল ব্যবহার করা হয় প্রোগ্রামটা কতটুকু ক্যাপেবল সেটা চেক করার জন্য।
আমরা উদাহরণ দেখি দুই একটা। প্রথম উদাহরণ Mr. Raymond Smullyan নামে একজন ভদ্রলোকের ক্রিয়েট করা পাজল, যাঁকে মাস্টার অফ লজিক পাজল বলা হয়।
- উদাহরণ - ১ঃ In [Sm78] Smullyan posed many puzzles about an island that has two kinds of inhabitants, knights, who always tell the truth, and their opposites, knaves, who always lie. You encounter two people A and B. What are A and B if A says “B is a knight” and B says “The two of us are opposite types”?
এখানে বলা হচ্ছে একটা দ্বীপে দুই ধরণের অধিবাসী আছে। একটা হলো নাইটস যারা সবসময় সত্যি কথা বলে এবং অন্যটা হলো knaves বা ঠগ যারা সবসময় মিথ্যা কথা বলে। আমি দুইজনকে পেলাম যাদের নাম A এবং B. আমাদের বের করতে হবে এরা কারা? A বলছে B একজন নাইট। আবার B বলছে আমরা দুইজন একজন আরেকজনের বিপরীত ধরণের।
ধরি p হলো A is a knight এবং q হলো B is a knight. তার মানে ¬p এবং ¬q হবে A is a knave এবং B is a knave.
আমরা প্রথমে ধরে নিলাম A একজন নাইট। তার মানে p true। যদি A নাইট হয় তাহলে সে সত্যি বলছে যে B ও একজন নাইট। তার মানে এরা দুইজনই একই টাইপের। কিন্তু যদি B একজন নাইট হয় তাহলে B এর স্টেটমেন্ট অর্থাৎ (p ∧ ¬q) ∨ (¬p ∧ q) true হতে পারে না। কারণ এরা দুইজনই নাইট। সেক্ষেত্রে B এর স্টেটমেন্ট ফলস, তার মানে B একজন knave। আর যেহেতু B একজন knave তার মানে A এর স্টেটমেন্টও true না। তার মানে সেও একজন knave. সুতরাং A এবং B দুইজনই knave.
Logic Circuits
প্রোপোজিশনাল লজিক কম্পিউটার হার্ডওয়্যারের ডিজাইনেও ব্যবহৃত হয়। আমরা ১২ নম্বর পার্টে লজিক সার্কিট নিয়ে আরো ভালভাবে শিখবো। এখানে জাস্ট একটা সংক্ষিপ্ত বর্ণনা দেয়ার চেষ্টা করছি।
একটা লজিক সার্কিট (বা ডিজিটাল সার্কিট) এক বিট করে p1, p2, p3, ..., pn ইনপুট সিগন্যালস রিসিভ করে এবং এক বিট করে s1, s2, s3, ..., sn আউটপুট প্রডিউস করে। আমরা আপাতত একটা আউটপুটেই স্ট্রিক্ট থাকবো। কিন্তু জেনে রাখুন মাল্টিপল আউটপুটও দিতে পারে একটা সার্কিট।
কমপ্লিকেটেড সার্কিট মূলত তিনটা বেসিক সার্কিটের সমন্বয়ে গঠিত হয়। এদেরকে বলা হয় Gates।
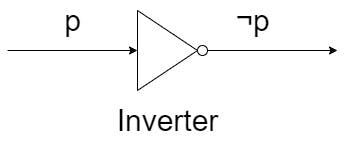
- Inverter or NOT gate - এই গেইট যদি ইনপুট হিসেবে p নেয় তাহলে আউটপুট দিবে ¬p.
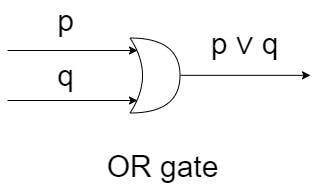
- OR gate - এই গেইটে ইনপুট হিসেবে যাবে p এবং q, আউটপুট পাসবে p ∨ q.
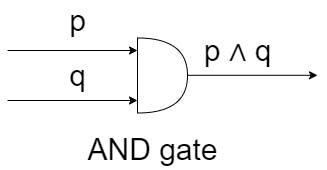
- AND gate - এই গেইটে p ও q এর ইনপুটের বিপরীতে p ∧ q আউটপুট আসবে।
আমরা কম্বিনেশনাল সার্কিট দেখি। ব্যাপারটা ক্লিয়ার হয়ে যাবে তাহলে।
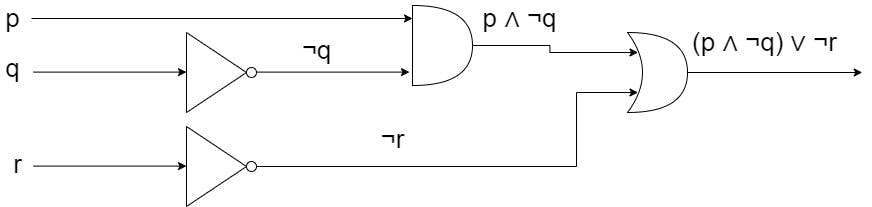
এখানে ৩টা ইনপুট আছে। p, q, r। q, r ইনভার্টারে ঢুকে ¬q এবং ¬r হয়ে বের হবে। ¬q একটা AND gate এ ইনপুট হিসেবে যাচ্ছে এবং p ও সেই একই AND gate এ ইনপুট হিসেবে গিয়ে p ∧ ¬q আউটপুট হিসেবে বের হবে। বের হয়ে সে একটা OR gate এ গেছে এবং ¬r ও সেই একই গেইটে গেছে। ফাইনালি (p ∧ ¬q) ∨ ¬r আউটপুট হিসেবে আমরা পাবো। বইয়ে আরেকটা উদাহরণ আছে সেটা আপনারা নিজেরা চেষ্টা করবেন। সাথে সাথে এক্সারসাইজগুলোও করবেন। আমরা লজিক সার্কিটা সম্পর্কে পরবর্তীতে আরো ডিটেইলস জানবো। এটা শুধুমাত্র একটা ধারণা দিয়ে রাখলাম।
Conclusion
গত আর্টিকেলে প্রোপরশনাল লজিক নিয়ে আলোচনা করলেও এগুলো কি কি কাজে লাগে তা নিয়ে বলা হয়নি। কিন্তু আজকের আর্টিকেল পড়ার পর আপনারা বুঝতেই পারছেন প্রোপোজিশনাল লজিক কতটা গুরুত্বপুর্ণ কম্পিউটার সায়েন্সে। আপনারা যত প্র্যাকটিস করবেন ততোই আরো ভালভাবে এগুলো বুঝতে পারবেন। আশা করবো সবাই বই এবং অন্যান্য রিসোর্স ঘেঁটে আরো ভালভাবে স্টাডি করবেন। পরবর্তী আর্টিকেলে আমরা Propositional Equivalences নিয়ে আলোচনা করবো। ততক্ষণ পর্যন্ত হ্যাপি লার্নিং। 😊😊

